The modern synthesis of genetics and evolution

As mentioned at the beginning of the previous chapter, mechanisms of inheritance, or genetics, were not understood at the time Charles Darwin and Alfred Russel Wallace were developing their idea of natural selection. This lack of understanding was a stumbling block to understanding many aspects of evolution. In fact, the predominant (and incorrect) genetic theory of the time, blending inheritance, made it difficult to understand how natural selection might operate. Darwin and Wallace were unaware of the genetics work by Austrian monk Gregor Mendel, which was published in 1866, not long after publication of Darwin’s book, On the Origin of Species. Mendel’s work was rediscovered in the early twentieth century at which time geneticists were rapidly coming to an understanding of the basics of inheritance. Initially, the newly discovered particulate nature of genes made it difficult for biologists to understand how gradual evolution could occur. But over the next few decades genetics and evolution were integrated in what became known as the modern synthesis—the coherent understanding of the relationship between natural selection and genetics that took shape by the 1940s and is generally accepted today. In sum, the modern synthesis describes how evolutionary processes, such as natural selection, can affect a population’s genetic makeup, and, in turn, how this can result in the gradual evolution of populations and species.

Population Genetics

Recall that a gene for a particular character may have several alleles, or variants, that code for different traits associated with that character. For example, in the ABO blood type system in humans, three alleles determine the particular blood-type protein on the surface of red blood cells. Each individual in a population of diploid organisms can only carry two alleles for a particular gene, but more than two may be present in the individuals that make up the population. Mendel followed alleles as they were inherited from parent to offspring. In the early twentieth century, biologists in a field of study known as population genetics began to study how selective forces change a population through changes in allele and genotypic frequencies.

The allele frequency (or gene frequency) is the rate at which a specific allele appears within a population. Until now we have discussed evolution as a change in the characteristics of a population of organisms, but behind that phenotypic change is genetic change. In population genetics, the term evolution is defined as a change in the frequency of an allele in a population. Using the ABO blood type system as an example, the frequency of one of the alleles, IA, is the number of copies of that allele divided by all the copies of the ABO gene in the population. For example, a study in Jordan found the frequency of IA to be 26.1 percent (Hanania, Hassawi, & Irshaid, 2007). The IB and I0 alleles made up 13.4 percent and 60.5 percent of the alleles respectively, and all of the frequencies added up to 100 percent. A change in this frequency over time would constitute evolution in the population.

The allele frequency within a given population can change depending on environmental factors; therefore, certain alleles become more widespread than others during the process of natural selection. Natural selection can alter the population’s genetic makeup; for example, if a given allele confers a phenotype that allows an individual to better survive or have more offspring. Because many of those offspring will also carry the beneficial allele, and often the corresponding phenotype, they will have more offspring of their own that also carry the allele, thus, perpetuating the cycle. Over time, the allele will spread throughout the population. Some alleles will quickly become fixed in this way, meaning that every individual in the population will carry the allele, while detrimental mutations may be swiftly eliminated if derived from a dominant allele from the gene pool. The gene pool is the sum of all the alleles in a population.

Sometimes, allele frequencies within a population change randomly with no advantage to the population over existing allele frequencies. This phenomenon is called genetic drift. Natural selection and genetic drift usually occur simultaneously in populations and are not isolated events. It is hard to determine which process dominates because it is often nearly impossible to determine the cause of change in allele frequencies at each occurrence. An event that initiates an allele frequency change in an isolated part of the population, which is not typical of the original population, is called the founder effect. Natural selection, random drift, and founder effects can lead to significant changes in the genome of a population.

Hardy-Weinberg Principle of Equilibrium

In the early twentieth century, English mathematician Godfrey Hardy and German physician Wilhelm Weinberg stated the principle of equilibrium to describe the genetic makeup of a population. The theory, which later became known as the Hardy-Weinberg principle of equilibrium, states that a population’s allele and genotype frequencies are inherently stable— unless some kind of evolutionary force is acting upon the population, neither the allele nor the genotypic frequencies would change. The Hardy-Weinberg principle assumes conditions with no mutations, migration, emigration, or selective pressure for or against genotype, plus an infinite population. While no population can satisfy those conditions, the principle offers a useful model against which to compare real population changes.

Working under this theory, population geneticists represent different alleles as different variables in their mathematical models. The variable p represents the dominant allele in the population while the variable q represents the recessive allele. For example, when looking at Mendel’s peas, the variable p represents the frequency of y alleles that confer the color yellow and the variable q represents the frequency of y alleles that confer the color green. If these are the only two possible alleles for a given locus in the population, p + q = 1. In other words, all the p alleles and all the q alleles make up all of the alleles for that locus that are found in the population.

But what ultimately interests most biologists is not the frequencies of different alleles, but the frequencies of the resulting genotypes, known as the population’s genetic structure, from which scientists can surmise the distribution of phenotypes. If the phenotype is observed, only the genotype of the homozygous recessive alleles can be known; the calculations provide an estimate of the remaining genotypes.

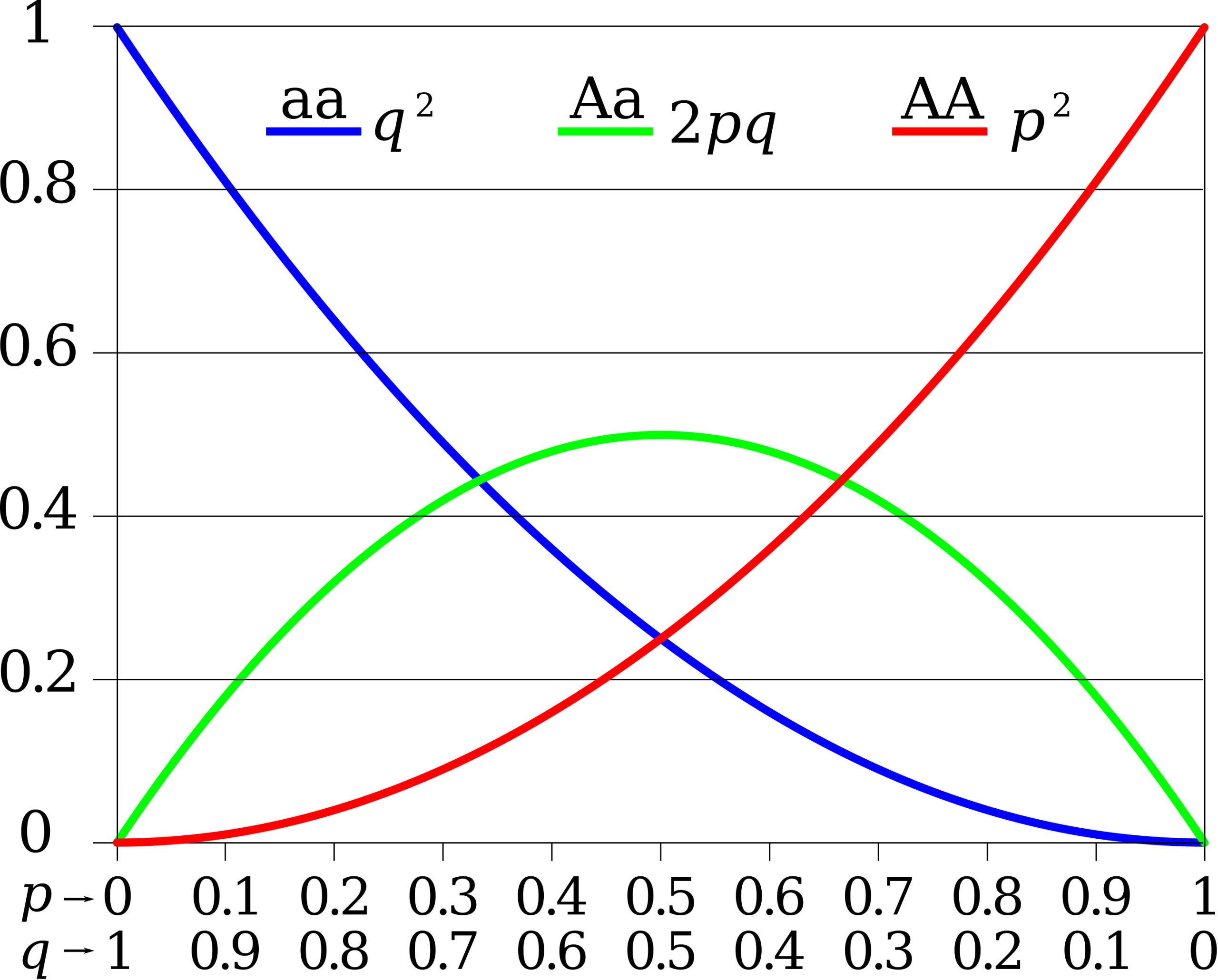
Since each individual carries two alleles per gene, if the allele frequencies (p and q) are known, predicting the frequencies of these genotypes is a simple mathematical calculation to determine the probability of getting these genotypes if two alleles are drawn at random from the gene pool. So in the above scenario, an individual pea plant could be pp (YY), and thus produce yellow peas; pq (Yy), also yellow; or qq (yy), and thus producing green peas (Fig 4). In other words, the frequency of pp individuals is simply p²; the frequency of pq individuals is 2pq; and the frequency of qq individuals is q². And, again, if p and q are the only two possible alleles for a given trait in the population, these genotype frequencies will sum to one: p² + 2pq + q² = 1.

Figure 4: When populations are in Hardy-Weinberg equilibrium, the allelic frequency is stable from generation to generation and the distribution of alleles can be determined from the Hardy-Weinberg equation. If the allelic frequency measured in the field differs from the predicted value, scientists can make inferences about what evolutionary forces are at play. (credit: “Hardy-Weinberg equilibrium” by OpenStax is licensed under CC BY 4.0)

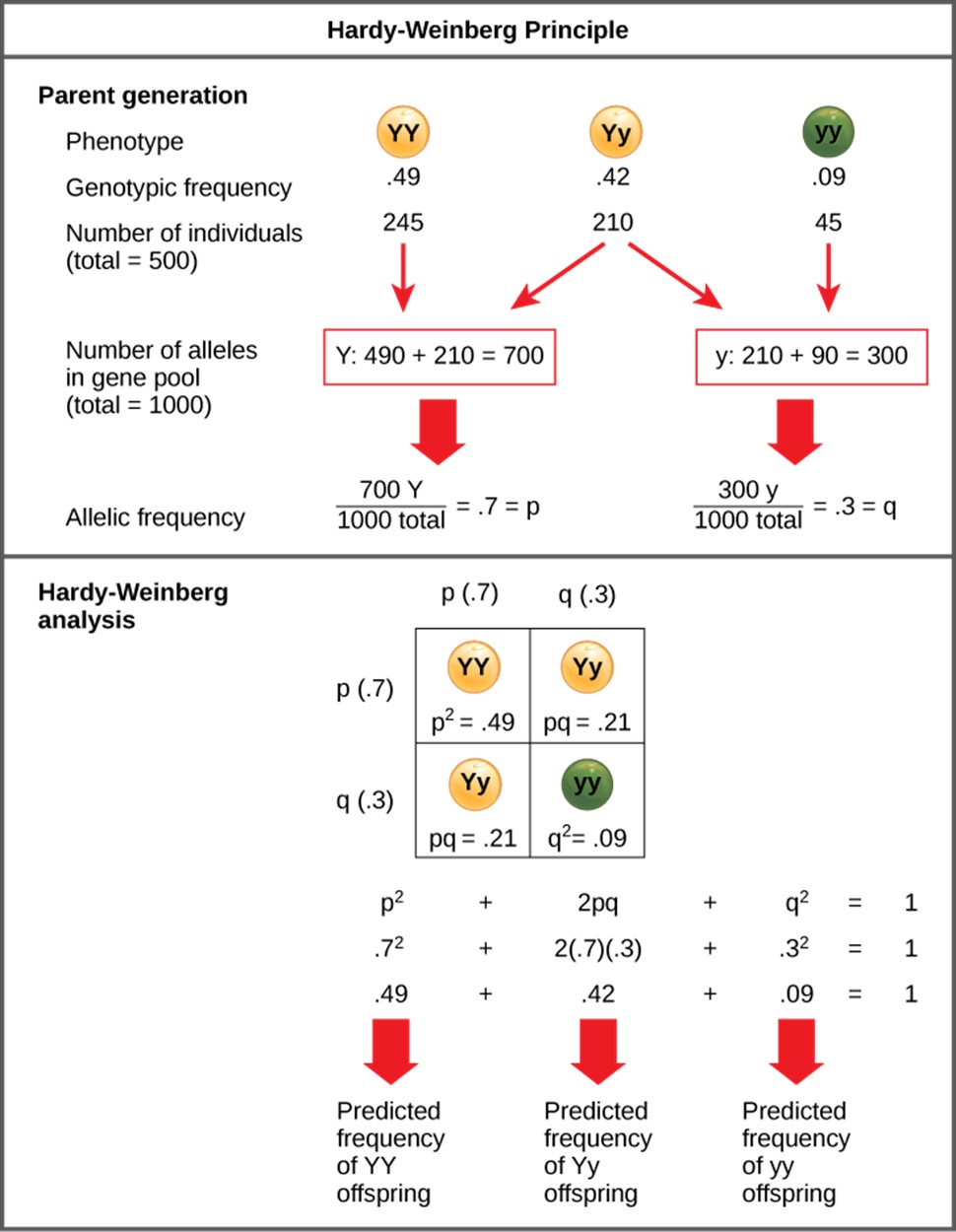
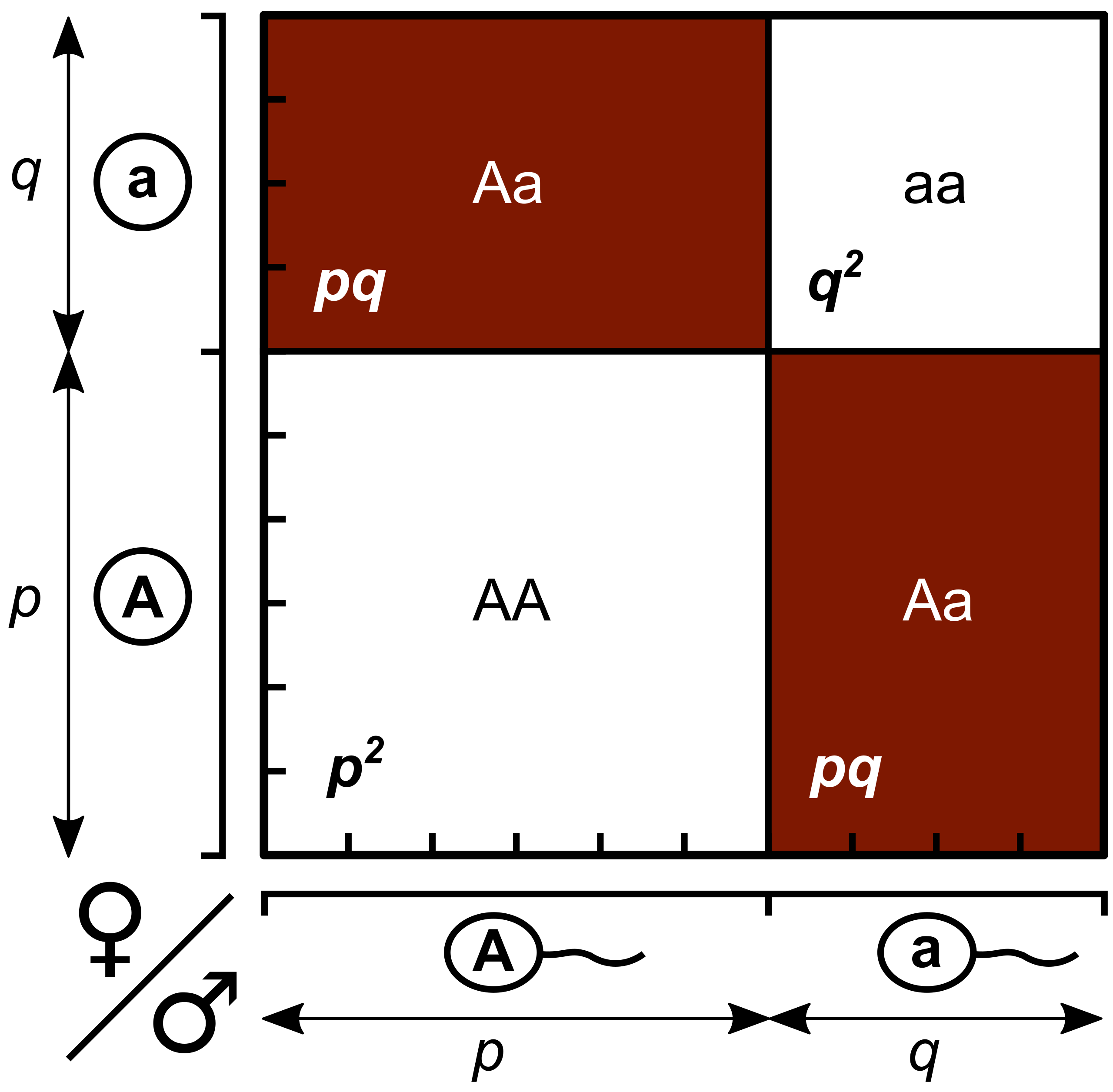
Another way to visualize the relationship between allele frequency and genotype frequency is a Punnett Square for Populations”. We can use these diagrams to help illustrate how predicted allele frequencies translate into predicted genotype frequencies across an entire population under the assumptions of the Hardy-Weinberg equilibrium (large, randomly mating population). For the gene with two alleles shown in Figure 5 (e.g., A and a), if the frequency of A is p and a is q.

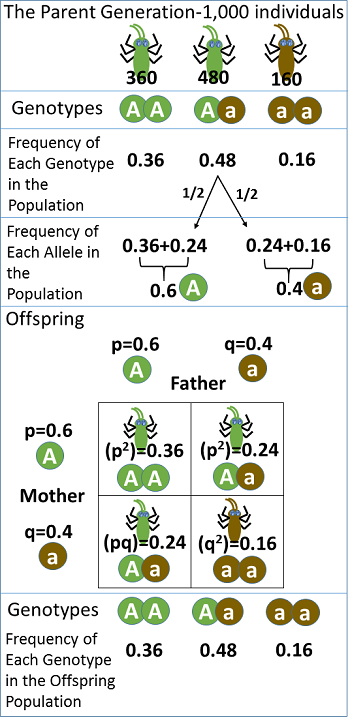
In the “Population Punnett Square” shown in Figure 6, the length of p and q corresponds to allele frequencies (here p = 0.6, q = 0.4). Then area of rectangle represents predicted genotype frequencies (thus AA : Aa : aa = 0.36 : 0.48 : 0.16).

Figure 6. Population Punnett Square. The length of p, q corresponds to allele frequencies, the area of rectangle represents genotype frequencies (Image Credit: Noah A. Rosenberg and Jonathan T. L. Kang; Wikimedia Commons).

In theory, if a population is at equilibrium—that is, no evolutionary forces are acting upon it—generation after generation would have the same gene pool and genetic structure, and these equations would all hold true all of the time. Thus, when the Hardy-Weinberg equation is used in population genetics, it is assumed that a constant allele frequency will be maintained over time. For this to occur it is implied that:

• The population is large
• There is random mating
• There is no mutation
• There is no gene flow (immigration or emigration)
• There is no natural selection or allele-specific mortality

Of course, even Hardy and Weinberg recognized that no natural population is immune to evolution. Populations in nature are constantly changing in genetic makeup due to drift, mutation, possibly migration, and selection. As a result, the only way to determine the exact distribution of phenotypes in a population is to go out and count them. The Hardy-Weinberg principle gives scientists a mathematical baseline of a non-evolving population to which they can compare evolving populations and thereby infer what evolutionary forces might be at play. If the frequencies of alleles or genotypes deviate from the value expected from the Hardy-Weinberg equation, then the population is evolving.

This video is a nice overview of Hardy-Weinberg Equilibrium.

Violations of Hardy-Weinberg

Remember, that the Hardy-Weinberg principle posits that if a population is not affected by mutation, selection, migration, or genetic drift, and if random mating occurs, the frequencies of alleles and genotypes will remain in equilibrium across generations. In this idealized state, the frequencies of two alleles ‘A’ (dominant) and ‘a’ (recessive) are represented by ‘p’ and ‘q’, respectively. The principle provides a mathematical formula to predict genotype frequencies:

p² + 2pq + q² = 1

where:

• p² represents the proportion of individuals with the homozygous dominant genotype (AA),
• 2pq represents the proportion of individuals with the heterozygous genotype (Aa),
• q² represents the proportion of individuals with the homozygous recessive genotype (aa).

This model assumes that the sum of all allele frequencies equals 1 (i.e., p+q=1).

 

In evolutionary biology, the Hardy-Weinberg principle provides a theoretical baseline against which real-world genetic data can be compared. By analyzing deviations (that is, violations) from equilibrium, researchers can infer the presence of evolutionary forces or population-level changes:

• Natural Selection: If certain genotypes are found at higher or lower frequencies than expected, this can indicate that natural selection is favoring or disfavoring specific alleles. For instance, in a changing environment, certain traits may confer a selective advantage, leading to changes in allele frequencies.
• Genetic Drift: Small, isolated populations are particularly prone to random fluctuations in allele frequencies, known as genetic drift. Comparing genetic data to the Hardy-Weinberg equilibrium helps identify the impact of drift, which can lead to reduced genetic diversity or fixation of alleles.
• Gene Flow: Migration between populations can introduce new alleles and homogenize genetic differences. Significant deviations from expected allele frequencies can reveal historical or ongoing migration events that impact local genetic structure.
• Non-Random Mating: Mate choice preferences, inbreeding, or assortative mating can alter genotype frequencies, often increasing the proportion of homozygous individuals. These patterns can be detected through a Hardy-Weinberg Equilibrium analysis.
• Mutation: Although mutations are relatively rare, they provide the raw genetic material for evolution. If new mutations confer an adaptive advantage, they may increase in frequency over time, creating a noticeable deviation from Hardy-Weinberg expectations.
• Population Bottlenecks and Founder Effects: Events like population bottlenecks or founder effects can drastically alter genetic variation. Comparing the genetic composition of populations before and after such events reveals the long-term impacts on allele frequencies.

This video has some nice examples of violations of Hardy-Weinberg in the study population of genetics.

Use this online calculator to determine the genetic structure of a population (relationship between allele and genotype frequencies).

Hardy Weinberg Examples

Let’s take a look at how to solve some problems together.  There are two important “rules” to keep in mind.  Firstly, always start with the recessive.  Because there is only one genotype to express the recessive version of the trait, it makes it clear.  (With the dominant version of a trait there are two possible genotypes – homozygous dominant and heterozygous – this complicates things a bit, so we wait to determine what is going on with these genotypes until after we figure out the recessive).

Secondly, remember that a genotype or expression of a trait is dictated by two alleles and therefore the equation that deals with 2 alleles is for traits, individuals, genotypes.  That is the expression p² + 2pq + q² = 1 will deal with genotypes and traits you can see (like black cats, or crooked fingers, etc.).  If you are trying to determine an allele, then you just focus on one piece of information (for example, “p” for the dominant allele).

Example #1

A population of crickets is composed of both loud chirpers and soft chirpers.  This trait is determined by genes, with the loud chirping allele being dominant to the soft chirping allele.

There are 48 loud chirpers and 14 soft chirpers in the population.  What percentage of crickets is heterozygous for loud chirping?

Step 1:  Start with the recessive

We need to know what % of the population are soft chirpers.  14 crickets out of a total of 62 animals.  Since these are individuals and since it is a genotype we are looking at q².  That means 14/62 or 0.225 are soft chirpers.

Step 2:  What is the recessive allele frequency?

Since 0.225 is q², we can take the square root of this to get q.  This value is 0.474.

Step 3:  Now that we have the recessive allele frequency, determine the dominant allele frequency.

Use the equation p + q = 1 and rearrange to be p = 1 – q

We know that q is 0.474 so plug this in

p = 1 – 0.474 = 0.526

Step 4: Determine what part of the equation you need to solve for and then answer the question

We need to know what the heterozygous frequency is so we are looking at 2pq

We have p and q determined already so we just need to plug in the values.

2 X 0.526 X 0.474 = 0.498

This means that ~50% (rounding up) of the cricket population is heterozygous for loud chirping.

Example #2

In a population of 162 rabbits, 34 of them express a recessive trait.  What is the allelic frequency for this trait?  Assuming Hardy-Weinberg equilibrium, how many rabbits would you expect to have the recessive trait the following year when 250 rabbits are present?

Step 1: Start with the recessive and find the recessive allele frequency

34 out of 162 have the recessive genotype or trait.  That means that 0.209 or ~21% of the rabbits have this recessive trait.  This is the q² value.

To find the allelic frequency, you need to take the square root of 0.21, which is 0.46.  This is q.

Step 2:  Apply this frequency to determine the prediction for the following year

Remember 0.46 is q (allele) and 0.21 is q² (genotype).  If we have 250 rabbits, we can use the percentage and apply it.

That is, we expect ~21% of the rabbits to have the recessive trait.

So 0.21 X 250 rabbits = 52.5 or 53 rabbits

If there is no evolution and equilibrium remains, we expect that 53 rabbits out of the 250 will be exhibiting the recessive trait

(As a double-check, you can take 53 out of 250 and you will find that 0.21 frequency for the recessive trait.  This tells us we did the problem correctly).

Questions

 

References

Hanania, S., Hassawi, D., and Irshaid, N. 2007. “Allele Frequency and Molecular Genotypes of ABO Blood Group System in a Jordanian Population,” Journal of Medical Sciences 7: 51-58, doi:10.3923/jms.2007.51.58.

Kosal, E. 2023. Introduction and Hardy Weinberg examples. NC State University.

OpenStax, Biology. OpenStax CNX. June 25, 2020. 19.1 Population Evolution found at https://openstax.org/books/biology/pages/19-1-population-evolution

OpenStax, Biology. OpenStax CNX. June 25, 2020. 19.3 Adaptive Evolution found at https://openstax.org/books/biology/pages/19-3-adaptive-evolution