6.2 Density dependence leads to logistic growth
Dawn Hart and OpenStaxCollege
Learning Objectives
By the end of this section, you will be able to:
- Compare and contrast density-dependent growth regulation and density-independent growth regulation, giving examples
- Link population growth models (e.g. exponential and logistic) to density-dependent and density-independent concepts
- Describe HOW the addition of resource limitation and density-dependence into the exponential growth model leads to the formation of the logistic growth model.
The logistic model of population growth, while valid in many natural populations and a useful model, is a simplification of real-world population dynamics. Implicit in the model is that the carrying capacity of the environment does not change, which is not the case. Carrying capacity can vary annually in some habitats: for example, carrying capacity during the winter can be lower than it is during the summer if these environmental factors have an impact on resource availability. Also, natural events such as earthquakes, volcanoes, and fires can alter an environment reducing available resources and hence its carrying capacity. Additionally, populations do not usually exist in isolation. They engage in inter-specific competition: that is, they share the environment with other species, competing with them for the same resources. While competition itself does not impact carrying capacity, it may suppress a population’s numbers below carrying capacity. These factors are important to understanding how a specific population will grow.
Nature regulates population growth in a variety of ways. These are grouped into density-dependent factors, in which the density (i.e. number of individuals per unit area) of the population at a given time affects growth rate and mortality, and density-independent factors, which influence growth rate and mortality in a population regardless of population density. Conservation biologists want to understand both types because this helps them manage populations and prevent extinction or overpopulation.
Density-dependent Regulation
Most density-dependent factors are biological in nature (biotic), and include predation, inter- and intraspecific competition, accumulation of waste, and diseases such as those caused by parasites. Usually, the denser a population is, the greater its mortality rate. For example, during intra- and interspecific competition, the reproductive rates of the individuals will usually be lower due to competition for food resources, reducing their population’s rate of growth. In addition, low prey density increases the mortality of its predator because it has more difficulty locating its food source.
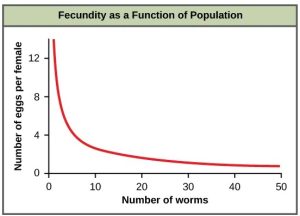
An example of density-dependent regulation is shown in (figure 6.3) with results from a study focusing on the giant intestinal roundworm (Ascaris lumbricoides), a parasite of humans and other mammals.1 Denser populations of the parasite exhibited lower fecundity: they contained fewer eggs. One possible explanation for this is that females would be smaller in more dense populations (due to limited resources) and that smaller females would have fewer eggs. This hypothesis was tested and disproved in a 2009 study which showed that female weight had no influence.2 The actual cause of the density-dependence of fecundity in this organism is still unclear and awaiting further investigation.
Figure 6.3 In this population of roundworms, fecundity (number of eggs) decreases with population density. [Image Description]
Density-independent Regulation and Interaction with Density-dependent Factors
Many factors, typically physical or chemical in nature (abiotic), influence the mortality of a population regardless of its density, including weather, natural disasters, and pollution. An individual deer may be killed in a forest fire regardless of how many deer happen to be in that area. Its chances of survival are the same whether the population density is high or low. The same holds true for cold winter weather.
In real-life situations, population regulation is very complicated and density-dependent and independent factors can interact. A dense population that is reduced in a density-independent manner by some environmental factor(s) will be able to recover differently than a sparse population. For example, a population of deer affected by a harsh winter will recover faster if there are more deer remaining to reproduce.
Resource limitation and density-dependence leads to logistic growth
The exponential growth model is based on the assumption that resources are unlimited. If resources are unlimited, then every individual in the population could obtain the resources needed to survive irrespective of how many individuals are in a particular habitat. In this way, the exponential growth model is a density-independent model. In reality, most natural populations do not exist in habitats with unlimited resources. Food, water, shelter, and mates are common limiting factors in many population and these limitations are more pronounced in larger populations compared to smaller populations (Figure 6.4).
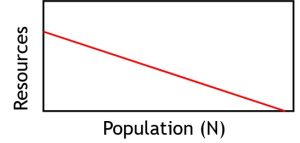
As we move from the exponential growth model to the logistic growth model, a major change is in the assumption regarding resource limitation. The exponential growth model assumes unlimited resources while the logistic growth model assumes resources are limiting. Since the logistic growth model assumes resource limitation which depends on population size, this is a density-dependent growth model. If we think about this further, we can conceptualize what might happen to population growth in small and large populations. In a small population, resource availability is high (Figure 6.4) and most individuals would have plentiful food, shelter, and water. This would likely lead to high birth rates and low death rates which would cause an increase in the overall population size. In a large population, resource availability is low (Figure 6.4) and most individuals would struggle to get enough to eat and drink or lack a place to seek shelter. This might lead to low birthrates and high death rates which would cause a decrease in the overall population size. The sweet spot in terms of population size would be an intermediate population size where the available resources are utilized but not over-utilized. At this population size the growth of the population would stabilize and the population would remain constant over time. This sweet spot would represent the carrying capacity of the population depicted in the logistic growth curve (Figure 6.1).
Section Summary
Populations are regulated by a variety of density-dependent and density-independent factors. Density dependent factors are often biotic and depend on population density. Examples include competition, predation, and disease. Density-independent factors are often abiotic and affect populations regardless of density. Examples include weather, pollution, and natural disasters. These factors can also interact to impact populations. For instance, a dense population hit by a harsh winter may recover faster than a sparse one due to more remaining individuals. Exponential growth assumes unlimited resources and is density-independent. Logistic growth accounts for resource limitations, making it density-dependent. In small populations, resources are abundant → high birth, low death rates → which leads to rapid growth. In large populations, resources are scarce → low birth, high death rates → which leads to slowed or negative growth. Populations stabilize at carrying capacity, where resource use is maximized without over exploitation.
Footnotes
1 N.A. Croll et al., “The Population Biology and Control of Ascaris lumbricoides in a Rural Community in Iran.” Transactions of the Royal Society of Tropical Medicine and Hygiene 76, no. 2 (1982): 187-197, doi:10.1016/0035-9203(82)90272-3.
2 Martin Walker et al., “Density-Dependent Effects on the Weight of Female Ascaris lumbricoides Infections of Humans and its Impact on Patterns of Egg Production.” Parasites & Vectors 2, no. 11 (February 2009), doi:10.1186/1756-3305-2-11.
Glossary
- density-dependent regulation
- regulation of population that is influenced by population density, such as crowding effects; usually involves biotic factors
- density-independent regulation
- regulation of populations by factors that operate independent of population density, such as forest fires and volcanic eruptions; usually involves abiotic factors
- interspecific competition
- competition between species for resources in a shared habitat or environment
Figure Descriptions
Figure 6.3. A line graph titled “Fecundity as a Function of Population.” The x-axis is Number of worms (0–50) and the y-axis is Number of eggs per female (0–13). A red curve starts high near 13 eggs at very low density, plunges steeply as worm number increases, and then flattens toward the x-axis by about 50 worms, illustrating strong negative density dependence. The higher population density corresponds to lower fecundity. [Return to Figure 6.3]
Media Attributions
- density dependent roundworm fecundity ch6.2 © Open Stax Biology 2e is licensed under a CC BY-NC (Attribution NonCommercial) license
- density dependent resource limitation © Dawn Hart is licensed under a CC BY-NC (Attribution NonCommercial) license
