Chapter 15 Equilibria of Other Reaction Classes
15.3 Lewis Acids and Bases
Learning Objectives
By the end of this section, you will be able to:
- Explain the Lewis model of acid-base chemistry
- Identify Lewis acids and Lewis bases based on structures
- Predict the product(s) of Lewis acid-base reactions
- Write equations for the formation of complex ions
- Perform equilibrium calculations involving formation constants
In 1923, G. N. Lewis proposed a generalized definition of acid-base behavior in which acids and bases are identified by their ability to accept or to donate a pair of electrons and form a coordinate covalent bond.
A coordinate covalent bond (or dative bond) occurs when one of the atoms in the bond provides both bonding electrons. For example, a coordinate covalent bond occurs when a water molecule combines with a hydrogen ion to form a hydronium ion. A coordinate covalent bond also results when an ammonia molecule combines with a hydrogen ion to form an ammonium ion. Both of these equations are shown here.
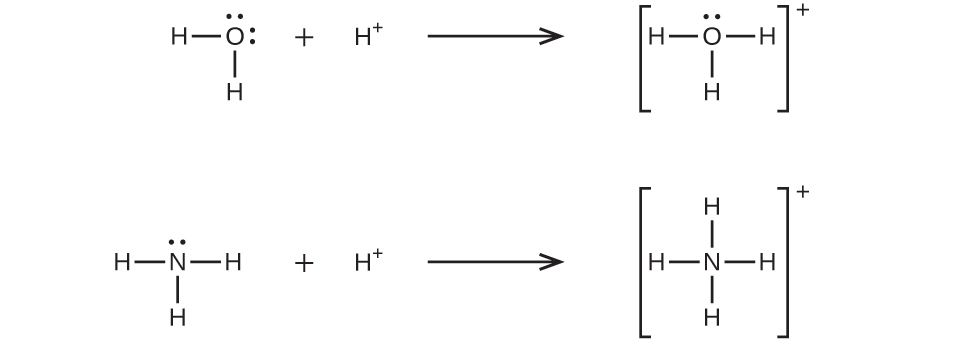
Reactions involving the formation of coordinate covalent bonds are classified as Lewis acid-base chemistry. The species donating the electron pair that compose the bond is a Lewis base (also called a nucleophile), the species accepting the electron pair is a Lewis acid (also called an electrophile), and the product of the reaction is a Lewis acid-base adduct. As the two examples above illustrate, Brønsted-Lowry acid-base reactions represent a subcategory of Lewis acid reactions, specifically, those in which the acid species is H+.
In order for Lewis acids to accept an electron pair, an atom must be electron deficient. This means the atom either is missing a full octet, in other words has an open octet, and/or is positively charged (either full charge or a partial charge). Lewis bases, on the other hand, must be electron rich in order to donate an electron pair. So Lewis bases must be negatively charged (either full charge or a partial charge) and typically have at least one lone pair.
Example 15.14 – Identifying Lewis Acids and Bases
Identify the following compounds as a Lewis acid or Lewis base.
(a) Ag+
(b) F–
(c) BF3
Solution
(a) Since Ag+ is positively charged, it is electron deficient and will be a Lewis acid.
(b) Since it has a negative charge and lone pairs, F– is electron rich and will be a Lewis base.
(c) The central boron in BF3 has only 3 bonds and no lone pair and has a open octet. Therefore, the boron is electron deficient and will be a Lewis acid.
Check Your Learning
Identify the following compounds as a Lewis acid or Lewis base.
(a) O2–
(b) Cu+
(c) NH3
Solution
(a) Lewis base (b) Lewis acid (c) Lewis base
A Lewis acid and a Lewis bas react when the Lewis base donates its electron pair to the Lewis acid. This pair of electron forms a new bond. Additionally, if the Lewis acid already has a full octet, a bond will also be broken simultaneously to avoid overfilling the atom accepting the electron pair. Which bond should be broken? The easiest type of bond to break is the weakest ones. These are π bonds. If the Lewis acid has no π bond, then
Example 15.15 – Predicting the Product(s) of Lewis Acid-Base Reactions
Predict the product(s) of the following Lewis acid-base reactions.
(a) F– + BF3 →
(b) 2 NH3 + Ag+ →
(c) O2– + SO3 →
Solution
Step 1: Identify the Lewis acid and base.
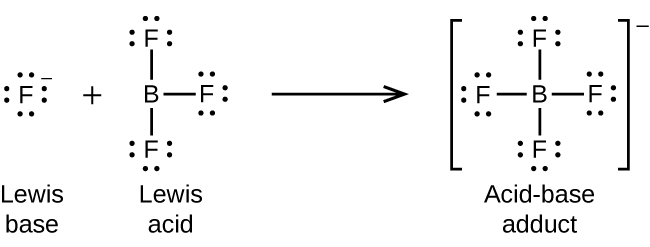
(a) The negatively charged F– is the Lewis base and BF3 the Lewis acid.
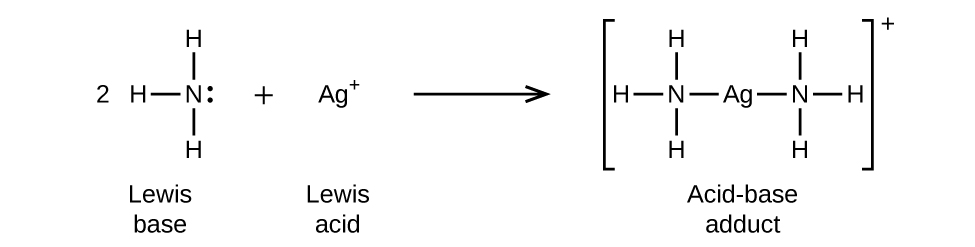
(b) The positively charged Ag+ is the Lewis acid and NH3 the Lewis base.
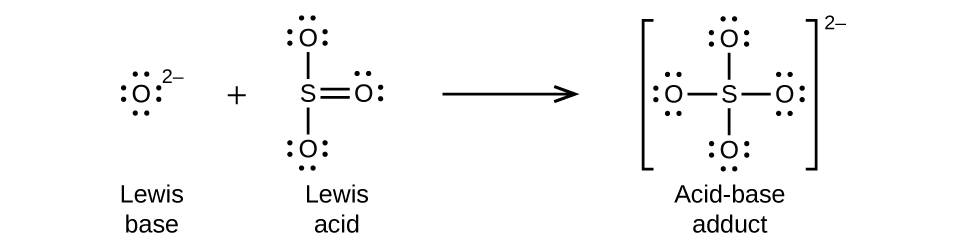
(c) The negatively charged O2– is the Lewis base and SO3 the Lewis acid.
Step 2: Predict the product(s) by donating an electron pair from the Lewis base to the Lewis acid.
(a) The fluoride donates its lone pair to the boron of BF3, which has an open octet. Since the boron does not have a full octet, no bond needs to be broken. So the final product is BF4–.
(b) The nitrogen of ammonia, which has a lone pair and is δ–, donates its electron pair to the Ag+. (No bond break can take place since the Lewis acid is monoatomic.)
(c) Oxide donates its electron pair to the sulfur in SO3, which is δ+. Since the sulfur already has a lone pair, it needs to break a bond to avoid overfilling. Since there is a sulfur-oxygen double bond, which is weaker, the π bond is broken to form sulfate, SO42–.
Check Your Learning
Identify the following compounds as a Lewis acid or Lewis base.
(a) Cu2+ + 4 CN– →
(b) OH– + CH3Cl →
(c) CH3+ + H2O →
Solution
(a) Cu2+ + 4 CN– → Cu(CN)42–
(b) OH– + CH3Cl → HOCH3 + Cl–
(c) CH3+ + H2O → CH3OH2+
Many Lewis acid-base reactions are displacement reactions in which one Lewis base displaces another Lewis base from an acid-base adduct, or in which one Lewis acid displaces another Lewis acid:
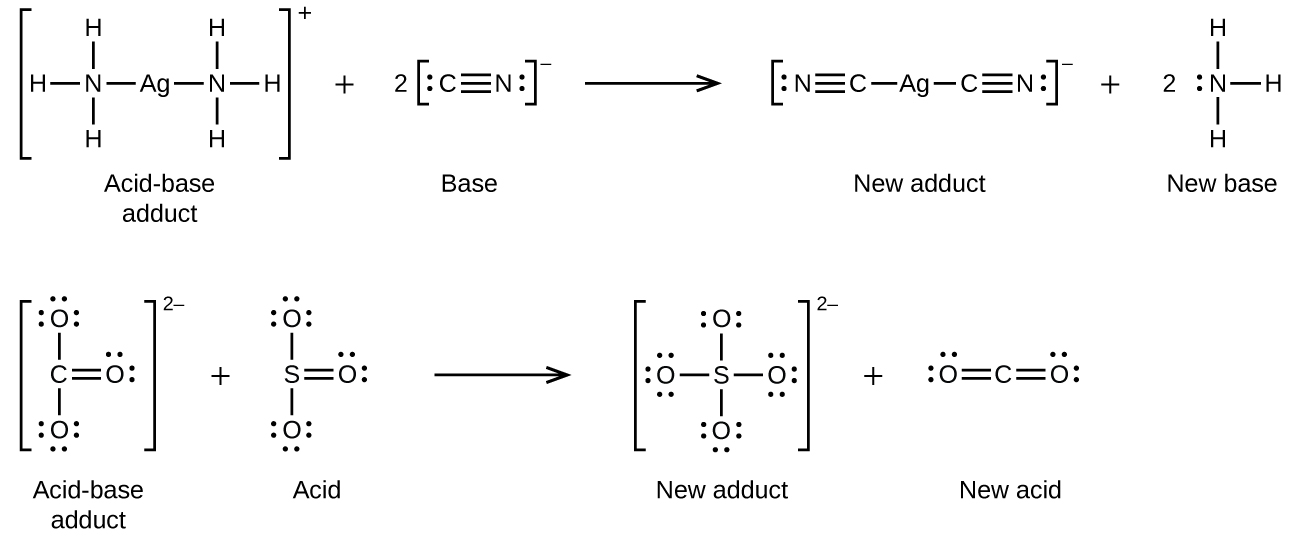
Another type of Lewis acid-base chemistry involves the formation of a complex ion (or a coordination complex) comprising a central atom, typically a transition metal cation, surrounded by ions or molecules called ligands. These ligands can be neutral molecules like H2O or NH3, or ions such as CN– or OH–. Often, the ligands act as Lewis bases, donating a pair of electrons to the central atom. These types of Lewis acid-base reactions are examples of a broad subdiscipline called coordination chemistry—the topic of another chapter in this text.
The equilibrium constant for the reaction of a metal ion with one or more ligands to form a coordination complex is called a formation constant (Kf) (sometimes called a stability constant). For example, the complex ion Cu(CN)2−
is produced by the reaction
The formation constant for this reaction is
Alternatively, the reverse reaction (decomposition of the complex ion) can be considered, in which case the equilibrium constant is a dissociation constant (Kd). Per the relation between equilibrium constants for reciprocal reactions described, the dissociation constant is the mathematical inverse of the formation constant, Kd = Kf–1. A tabulation of formation constants is provided in Appendix K.
As an example of dissolution by complex ion formation, let us consider what happens when we add aqueous ammonia to an aqueous solution of silver chloride. Silver chloride dissolves slightly in water, giving a small concentration of Ag+ ([Ag+] = 1.3 × 10–5 M):
However, if NH3 is present in the water, the complex ion, Ag(NH3)2+, can form according to the equation:
with
The large size of this formation constant indicates that most of the free silver ions produced by the dissolution of AgCl combine with NH 3 to form Ag(NH3)2+. As a consequence, the concentration of silver ions, [Ag+], is reduced, and the reaction quotient for the dissolution of silver chloride, [Ag+][Cl–], falls below the solubility product of AgCl:
More silver chloride then dissolves. If the concentration of ammonia is great enough, all of the silver chloride dissolves.
Example 15.16 – Dissociation of a Complex Ion
Calculate the equilibrium concentration of silver ion (Ag+) in a solution that is initially 0.10 M Ag(NH3)2+.
Solution
Applying the standard ICE approach to this reaction yields the following:
| Ag+(aq) | + | 2 NH3(aq) | ⇌ | Ag(NH3)2+(aq) | |
| I (M) | 0 | 0 | 0.10 | ||
| C (M) | +x | +2x | −x | ||
| E (M) | x | 2x | 0.010 − x |
Substituting these equilibrium concentration terms into the Kf expression gives
Using this value of x and the relations in the above ICE table allows calculation of all species’ equilibrium concentrations:
Check Your Learning
Calculate the silver ion concentration, [Ag+], of a solution prepared by dissolving 1.00 g of AgNO3 and 10.0 g of KCN in sufficient water to make 1.00 L of solution.
Click here for some hints!
Dissolution of AgNO3 produces Ag+ and NO3− ions, while dissolution of KCN produces K+ and CN− ions. The complex ion formed is Ag(CN)2− (Kf = 1 × 1021, Appendix K).
Because Kf is very large, assume the reaction goes to completion; then calculate the [Ag+] produced by dissociation of the complex.
Click here for the solution!
First, we calculate the mols of Ag+ and CN− present in the solution:
[latex]n_{Ag^+}=n_{AgNO_3}=\frac{1.00\ g\ AgNO_3}{169.87\ \frac{g}{mol}\ AgNO_3}=0.00589\ \text{mol}[/latex]
[latex]n_{CN^-}=n_{KCN}=\frac{10.0\ g\ KCN}{65.12\ \frac{g}{mol}\ KCN}=0.154\ \text{mol}[/latex]
Because Kf is very large, we start by assuming that the formation of Ag(CN)2− goes to completion:
| Ag+(aq) | + | 2 CN−(aq) | ⇌ | Ag(CN)2−(aq) | |
| I (mol) | 0.00589 | 0.154 | 0 | ||
| C (mol) | −0.00589 | −2(0.00589) | +0.00589 | ||
| F (mol) | 0 | 0.142 | 0.00589 |
Because the total volume of the solution is 1 L, these values are equivalent to the molar concentrations. We can now use these “final” concentrations as the “initial” concentrations for an equilibrium problem. Applying the standard ICE approach to this reaction yields the following:
| Ag+(aq) | + | 2 CN−(aq) | ⇌ | Ag(CN)2−(aq) | |
| I (M) | 0 | 0.142 | 0.00589 | ||
| C (M) | +x | +2x | −x | ||
| E (M) | x | 0.142 + 2x | 0.00589 − x |
Substituting these equilibrium concentration terms into the Kf expression gives