Chapter 11 Solutions and Colloids
11.5 Colligative Properties
Learning Objectives
By the end of this section, you will be able to:
- Describe the effect of solute concentration on various solution properties (vapor pressure, boiling point, freezing point, and osmotic pressure)
- Perform calculations using the mathematical equations that describe these various colligative effects
- Describe the process of distillation and its practical applications
- Explain the process of osmosis and describe how it is applied industrially and in nature
The properties of a solution are different from those of either the pure solute(s) or solvent. Many solution properties are dependent upon the chemical identity of the solute. Compared to pure water, a solution of hydrogen chloride is more acidic, a solution of ammonia is more basic, a solution of sodium chloride is more dense, and a solution of sucrose is more viscous. There are a few solution properties, however, that depend only upon the total concentration of solute species, regardless of their identities. These colligative properties include vapor pressure lowering, boiling point elevation, freezing point depression, and osmotic pressure. This small set of properties is of central importance to many natural phenomena and technological applications, as will be described in this module.
Vapor Pressure Lowering
As described in the chapter on liquids and solids, the equilibrium vapor pressure of a liquid is the pressure exerted by its gaseous phase when vaporization and condensation are occurring at equal rates:
Dissolving a nonvolatile substance in a volatile liquid results in a lowering of the liquid’s vapor pressure. This phenomenon can be rationalized by considering the effect of added solute molecules on the liquid’s vaporization and condensation processes. To vaporize, solvent molecules must be present at the surface of the solution. The presence of solute decreases the surface area available to solvent molecules and thereby reduces the rate of solvent vaporization. Since the rate of condensation is unaffected by the presence of solute, the net result is that the vaporization-condensation equilibrium is achieved with fewer solvent molecules in the vapor phase (i.e., at a lower vapor pressure) (Figure 11.18).
While this interpretation is useful, it does not account for several important aspects of the colligative nature of vapor pressure lowering. A more rigorous explanation involves the property of entropy, a topic of discussion in a later chapter on thermodynamics. For purposes of understanding the lowering of a liquid’s vapor pressure, it is adequate to note that the more dispersed nature of matter in a solution, compared to separate solvent and solute phases, serves to effectively stabilize the solvent molecules and hinder their vaporization. This results in a lower vapor pressure and a correspondingly higher boiling point, as described in the next section of this module.
The relationship between the vapor pressures of solution components and the concentrations of those components is described by Raoult’s law: The partial pressure exerted by any component of an ideal solution is equal to the vapor pressure of the pure component multiplied by its mole fraction in the solution. The mathematical statement of Raoult’s law is as follows:
where PA is the vapor pressure of component A in the solution, PAo is the vapor pressure of pure A, and XA is the mole fraction of A in the solution.
Recalling that the total pressure of a gaseous mixture is equal to the sum of partial pressures for all its components (Dalton’s law of partial pressures), the total vapor pressure exerted by a solution containing i components is as follows:
A nonvolatile substance is one whose vapor pressure is negligible (Po ≈ 0), and so the vapor pressure above a solution containing only nonvolatile solutes is due only to the solvent:
(for a solution with only nonvolatile solutes)
Example 11.6 – Calculation of a Vapor Pressure
Compute the vapor pressure of an ideal solution containing 92.1 g of glycerin, C3H5(OH)3, and 184.4 g of ethanol, C2H5OH, at 40°C. The vapor pressure of pure ethanol is 0.178 atm at 40°C. Glycerin is essentially nonvolatile at this temperature.
Solution
Since the solvent is the only volatile component of this solution, its vapor pressure may be computed per Raoult’s law as:
First, calculate the molar amounts of each solution component using the provided mass data.
Next, calculate the mole fraction of the solvent (ethanol) and use Raoult’s law to compute the solution’s vapor pressure.
Check Your Learning
Click here to see a walkthrough for this problem!
First, we must calculate molar amounts of urea and water:
Next, we can calculate the mol fraction of water in the solution:
Finally, we can use Raoult’s law to calculate the vapor pressure of the solution:
Note that the math is simplified by the fact that only nonvolatile solutes are present in the solution.
Distillation of Solutions
Solutions whose components have significantly different vapor pressures may be separated by a selective vaporization process known as distillation. Consider the simple case of a mixture of two volatile liquids, A and B, with A being the more volatile liquid. Raoult’s law can be used to show that the vapor above the solution is enriched in component A; that is, the mole fraction of A in the vapor is greater than the mole fraction of A in the liquid (see end-of-chapter Exercise 65). By appropriately heating the mixture, component A may be vaporized, condensed, and collected—effectively separating it from component B.
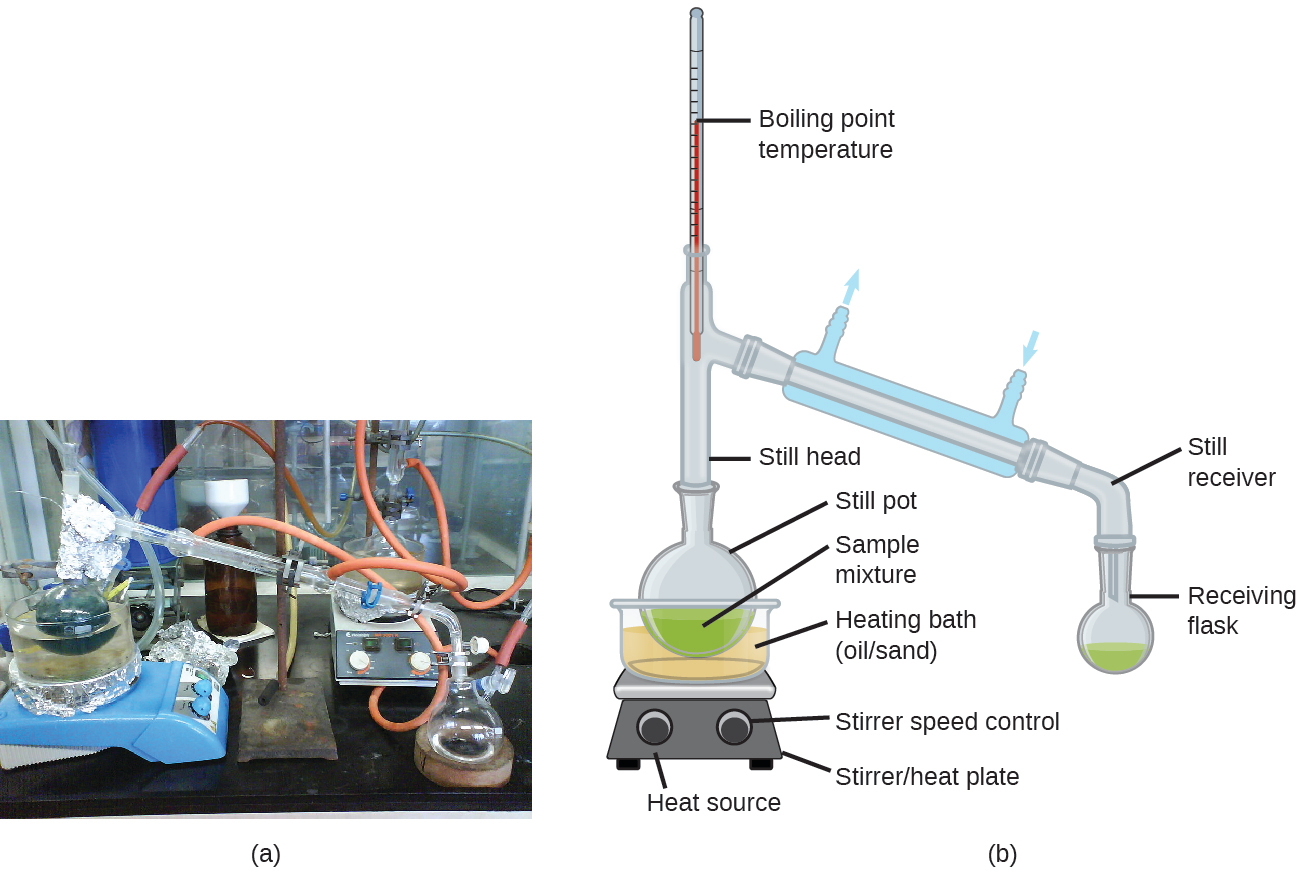
Distillation is widely applied in both laboratory and industrial settings, being used to refine petroleum, to isolate fermentation products, and to purify water. A typical apparatus for laboratory-scale distillations is shown in Figure 11.19.
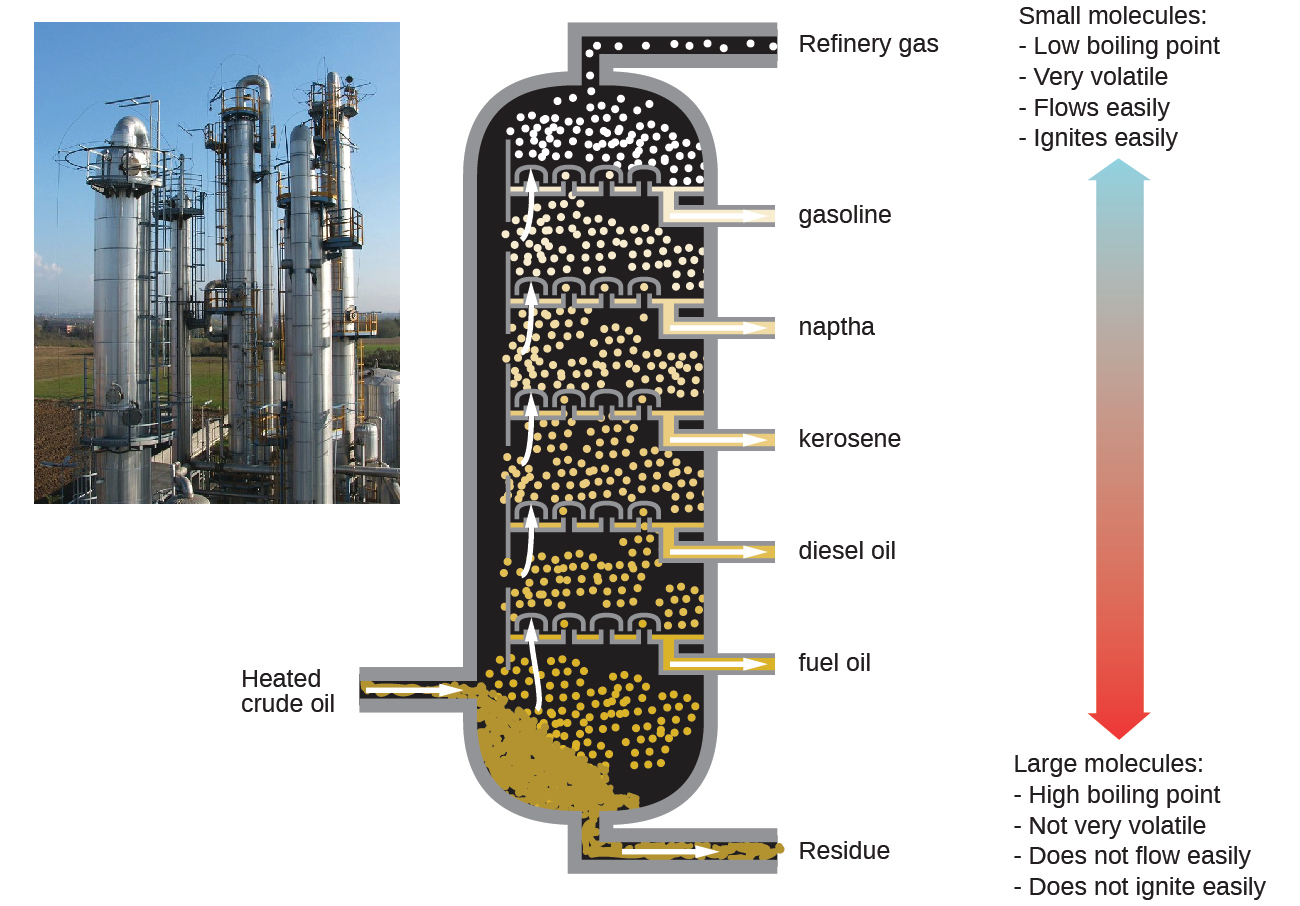
Oil refineries use large-scale fractional distillation to separate the components of crude oil. The crude oil is heated to high temperatures at the base of a tall fractionating column, vaporizing many of the components that rise within the column. As vaporized components reach adequately cool zones during their ascent, they condense and are collected. The collected liquids are simpler mixtures of hydrocarbons and other petroleum compounds that are of appropriate composition for various applications (e.g., diesel fuel, kerosene, gasoline), as depicted in Figure 11.20.
Boiling Point Elevation
As described in the chapter on liquids and solids, the boiling point of a liquid is the temperature at which its vapor pressure is equal to ambient atmospheric pressure. Since the vapor pressure of a solution is lowered due to the presence of nonvolatile solutes, it stands to reason that the solution’s boiling point will subsequently be increased. Vapor pressure increases with temperature, and so a solution will require a higher temperature than will pure solvent to achieve any given vapor pressure, including one equivalent to that of the surrounding atmosphere. The increase in boiling point observed when nonvolatile solute is dissolved in a solvent, ΔTb, is called boiling point elevation and is directly proportional to the molal concentration of solute species:
where Kb is the boiling point elevation constant and m is the molal concentration (molality) of all solute species.
Boiling point elevation constants are characteristic properties that depend on the identity of the solvent. Values of Kb for several solvents are listed in Table 11.2.
The extent to which the vapor pressure of a solvent is lowered and the boiling point is elevated depends on the total number of solute particles present in a given amount of solvent, not on the mass, size, or chemical identities of the particles. A 1 m aqueous solution of sucrose (342 g/mol) and a 1 m aqueous solution of ethylene glycol (62 g/mol) will exhibit the same boiling point because each solution has one mole of solute particles (molecules) per kilogram of solvent.
Example 11.7 – Calculating the Boiling Point of a Solution
Assuming ideal solution behavior, what is the boiling point of a 0.33 m solution of a nonvolatile solute in benzene?
Solution
Use the equation relating boiling point elevation to solute molality to solve this problem in two steps.
Step 1. Calculate the change in boiling point.
Step 2. Add the boiling point elevation to the pure solvent’s boiling point.
Check Your Learning
Click here to see a walkthrough for this problem!
Consulting table 11.2, we can find the Kb for water and calculate the boiling point elevation:
Then, we add the boiling point elevation to the pure solvent’s boiling point to calculate the boiling point of the solution:
Example 11.8 – The Boiling Point of an Iodine Solution
Find the boiling point of a solution of 92.1 g of iodine (I2) in 800.0 g of chloroform (CHCl3), assuming that the iodine is nonvolatile and that the solution is ideal.
Solution
A four-step approach to solving this problem is outlined below. 
Step 1. Convert from grams to moles of I2 using the molar mass of I2 in the unit conversion factor.
[latex]92.1\: g\: I_2 \left(\frac{1\: \text{mol}}{253.81\: g}\right)=0.363\: \text{mol}[/latex]
Step 2. Determine the molality of the solution from the number of moles of solute and the mass of solvent, in kilograms.
[latex]\frac{0.363\: \text{mol}}{0.800\: kg}=0.454\: m[/latex]
Step 3. Use the direct proportionality between the change in boiling point and molal concentration to determine how much the boiling point changes.
[latex]\Delta T_b=K_b\, m\ =\left(3.63\: \frac{^{\circ} \text{C}}{m} \right) \left( 0.454\: m\right) = 1.65 ^{\circ} \text{C}[/latex]
Step 4. Determine the new boiling point from the boiling point of the pure solvent and the change.
[latex]\text{boiling point} = 61.26 ^{\circ}\text{C}+1.65\ ^{\circ}\text{C}=62.91\ ^{\circ}\text{C}[/latex]
Check Your Learning
Click here for a walkthrough of this problem!
First, calculate the mols of glycerin:
[latex]1.0\: g\: \text{glycerin}\: \left(\frac{1\: \text{mol}}{92.094\: g}\right)=0.0109\: \text{mol}[/latex]
Then calculate the molality of the solution:
[latex]\frac{0.0109\: \text{mol}}{47.8\ g}\left(\frac{1000 \: g}{1\: kg} \right)=0.227\: m[/latex]
Next, calculate the boiling point elevation using Kb for water:
[latex]\Delta T_b=K_b\ m\ =\left(0.512 \frac{^{\circ}\text{C}}{m}\right)\left(0.227\ m\right)=0.116 ^{\circ}\text{C}[/latex]
Finally, calculate the boiling point of the solution:
[latex]\text{boiling point}=100.00\ ^{\circ}\text{C}+0.116\ ^{\circ}\text{C}=100.12\ ^{\circ}\text{C}[/latex]
Freezing Point Depression
Solutions freeze at lower temperatures than pure liquids. This phenomenon is exploited in “de-icing” schemes that use salt (Figure 11.21), calcium chloride, or urea to melt ice on roads and sidewalks, and in the use of ethylene glycol as an “antifreeze” in automobile radiators. Seawater freezes at a lower temperature than fresh water, so the Arctic and Antarctic oceans remain unfrozen even at temperatures well below 0°C (as do the body fluids of fish and other cold-blooded sea animals that live in these oceans).

The decrease in freezing point of a dilute solution compared to that of the pure solvent, ΔTf, is called the freezing point depression and is directly proportional to the molal concentration of the solute:
[latex]\Delta T_f = K_f \: m[/latex]
where m is the molal concentration of the solute and Kf is called the freezing point depression constant. Just as for boiling point elevation constants, these are characteristic properties whose values depend on the chemical identity of the solvent. Values of Kf for several solvents are listed in Table 11.2.
Example 11.9 – Calculation of the Freezing Point of a Solution
Assuming ideal solution behavior, what is the freezing point of the 0.33 m solution of a nonvolatile nonelectrolyte solute in benzene?
Solution
Use the equation relating freezing point depression to solute molality to solve this problem in two steps.

Step 1. Calculate the change in freezing point.
Step 2. Subtract the freezing point change observed from the pure solvent’s freezing point.
Check Your Learning
Click here for a walkthrough of this problem!
First, calculate the freezing point depression using the Kf value for nitrobenzene from table 11.2:
[latex]\Delta T_f=K_f\, m\ =\left(8.10\ \frac{^{\circ}\text{C}}{m}\right)\left(1.85\ m\right)=15.0\ ^{\circ}\text{C}[/latex]
Then subtract the freezing point depression from the freezing point of nitrobenzene:
[latex]\text{freezing point}=5.67\ ^{\circ}\text{C}-15.0\ ^{\circ}\text{C}=-9.3\ ^{\circ}\text{C}[/latex]
Chemistry in Everyday Life
Colligative Properties and De-Icing
Sodium chloride and its group 2 analogs calcium and magnesium chloride are often used to de-ice roadways and sidewalks, due to the fact that a solution of any one of these salts will have a freezing point lower than 0°C, the freezing point of pure water. The group 2 metal salts are frequently mixed with the cheaper and more readily available sodium chloride (“rock salt”) for use on roads, since they tend to be somewhat less corrosive than the NaCl, and they provide a larger depression of the freezing point, since they dissociate to yield three particles per formula unit, rather than two particles like the sodium chloride.
Because these ionic compounds tend to hasten the corrosion of metal, they would not be a wise choice to use in antifreeze for the radiator in your car or to de-ice a plane prior to takeoff. For these applications, covalent compounds, such as ethylene or propylene glycol, are often used. The glycols used in radiator fluid not only lower the freezing point of the liquid, but they elevate the boiling point, making the fluid useful in both winter and summer. Heated glycols are often sprayed onto the surface of airplanes prior to takeoff in inclement weather in the winter to remove ice that has already formed and prevent the formation of more ice, which would be particularly dangerous if formed on the control surfaces of the aircraft (Figure 11.22).

Phase Diagram for a Solution
The colligative effects on vapor pressure, boiling point, and freezing point described in the previous section are conveniently summarized by comparing the phase diagrams for a pure liquid and a solution derived from that liquid (Figure 11.23).
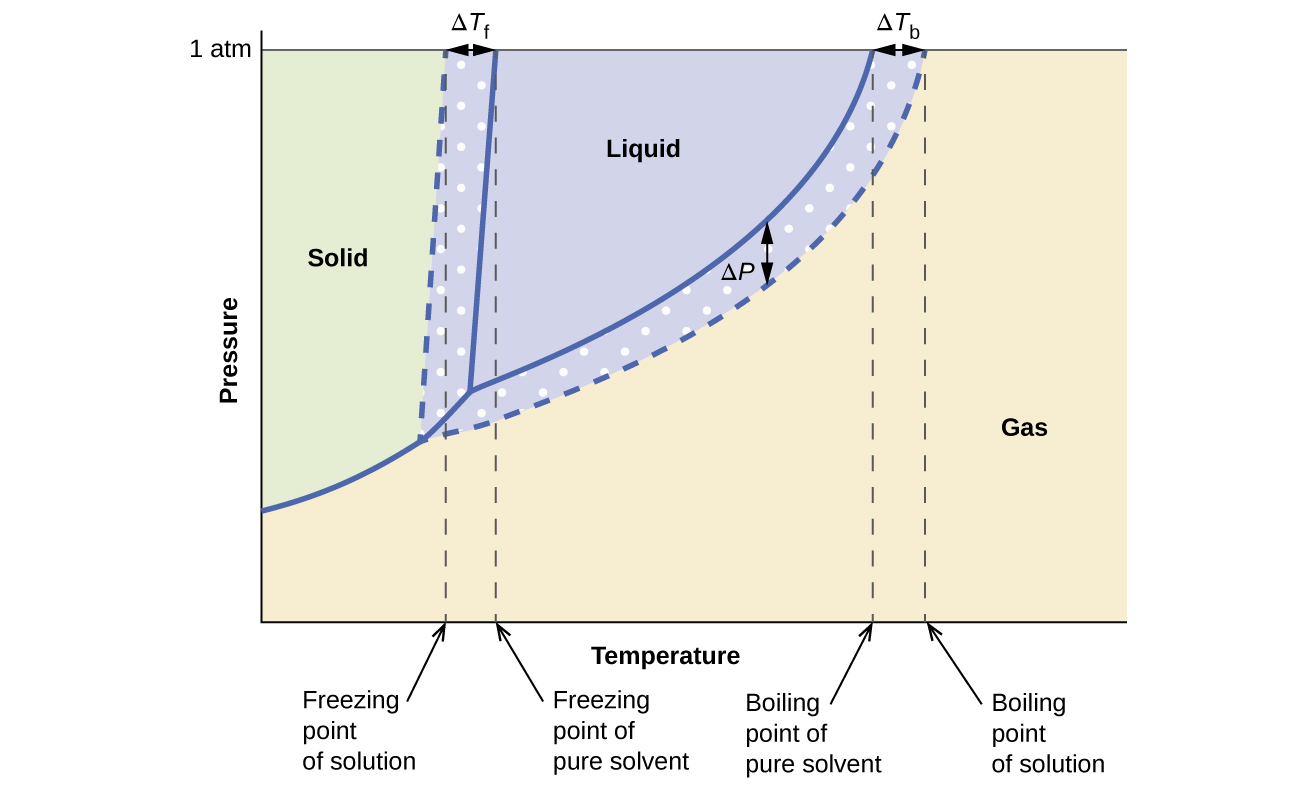
The liquid-vapor curve for the solution is located beneath the corresponding curve for the solvent, depicting the vapor pressure lowering, ΔP, that results from the dissolution of nonvolatile solute. Consequently, at any given pressure, the solution’s boiling point is observed at a higher temperature than that for the pure solvent, reflecting the boiling point elevation, ΔTb, associated with the presence of nonvolatile solute. The solid-liquid curve for the solution is displaced left of that for the pure solvent, representing the freezing point depression, ΔTf, that accompanies solution formation.
Finally, notice that the solid-gas curves for the solvent and its solution are identical. This is the case for many solutions comprising liquid solvents and nonvolatile solutes. Just as for vaporization, when a solution of this sort is frozen, it is actually just the solvent molecules that undergo the liquid-to-solid transition, forming pure solid solvent that excludes solute species. The solid and gaseous phases, therefore, are composed of solvent only, and so transitions between these phases are not subject to colligative effects.
Osmosis and Osmotic Pressure of Solutions
A number of natural and synthetic materials exhibit selective permeation, meaning that only molecules or ions of a certain size, shape, polarity, charge, and so forth, are capable of passing through (permeating) the material. Biological cell membranes provide elegant examples of selective permeation in nature, while dialysis tubing used to remove metabolic wastes from blood is a more simplistic technological example. Regardless of how they may be fabricated, these materials are generally referred to as semipermeable membranes.
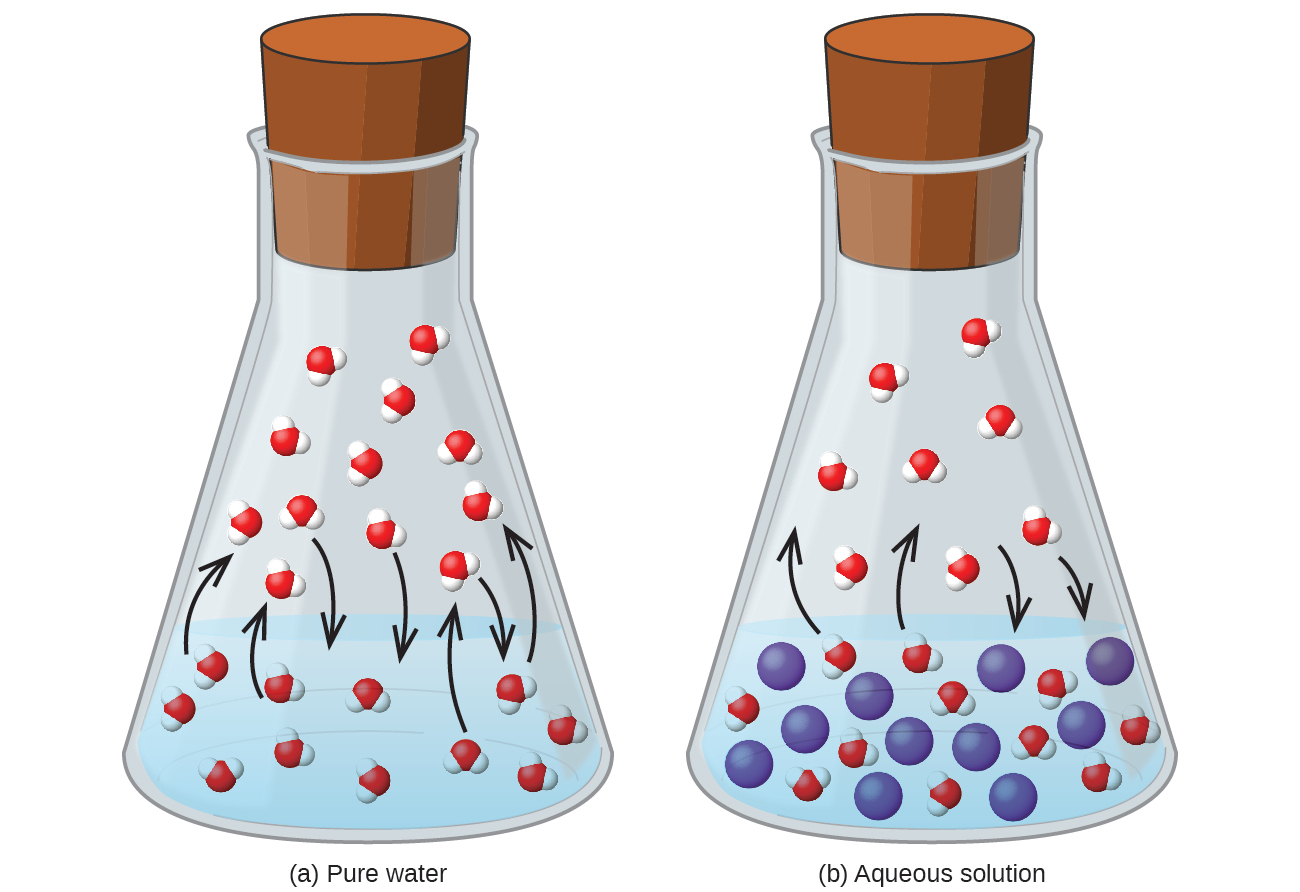
Consider the apparatus illustrated in Figure 11.24, in which samples of pure solvent and a solution are separated by a membrane that only solvent molecules may permeate. Solvent molecules will diffuse across the membrane in both directions. Since the concentration of solvent is greater in the pure solvent than the solution, these molecules will diffuse from the solvent side of the membrane to the solution side at a faster rate than they will in the reverse direction. The result is a net transfer of solvent molecules from the pure solvent to the solution. Diffusion-driven transfer of solvent molecules through a semipermeable membrane is a process known as osmosis.
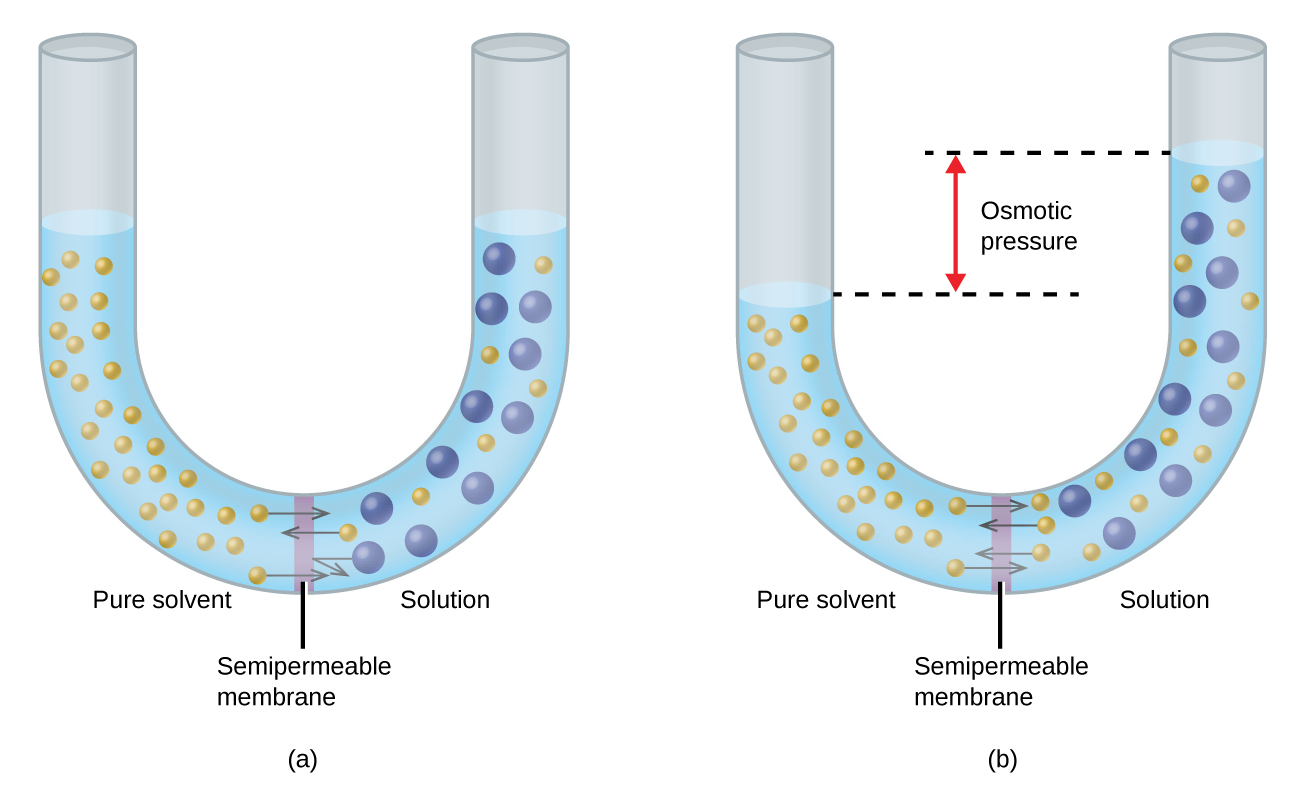
When osmosis is carried out in an apparatus like that shown in Figure 11.24, the volume of the solution increases as it becomes diluted by accumulation of solvent. This causes the level of the solution to rise, increasing its hydrostatic pressure (due to the weight of the column of solution in the tube) and resulting in a faster transfer of solvent molecules back to the pure solvent side. When the pressure reaches a value that yields a reverse solvent transfer rate equal to the osmosis rate, bulk transfer of solvent ceases. This pressure is called the osmotic pressure Π (biologist call this osmotic stress) of the solution. The osmotic pressure of a dilute solution is related to its solute molarity, M, and absolute temperature, T, according to the following equation:
Example 11.10 – Calculation of Osmotic Pressure
Assuming ideal solution behavior, what is the osmotic pressure (atm) of a 0.30 M solution of glucose in water that is used for intravenous infusion at body temperature, 37°C?
Solution
Find the osmotic pressure, Π, using the formula Π = MRT, where T is on the Kelvin scale (310 K) and the value of R is expressed in appropriate units (0.08206 L atm/mol K).
[latex]\Pi=MRT=\left(0.30\ \frac{\text{mol}}{L}\right)\left(0.08206\ \frac{L\ \cdot atm}{\text{mol}\ \cdot K}\right)\left(310\ K\right)=7.6\ atm[/latex]
Check Your Learning
Click here for a walkthrough of this problem!
First, calculate the mols of methanol:
[latex]5.0\ g\ \text{methanol}\ \left(\frac{1\ \text{mol}}{32.04\ g}\right)=0.16\ \text{mol}[/latex]
Next, calculate the molarity of the solution:
[latex]\frac{0.16\ \text{mol}}{0.750\ L}=0.21\ M[/latex]
Finally, calculate the osmotic pressure of the solution:
[latex]\Pi=MRT\ =\left(0.21\ \frac{\text{mol}}{L}\right)\left(0.08206\ \frac{L\ \cdot atm}{mol\ \cdot K}\right)\left(310\ K\right)=5.3\ atm[/latex]
If a solution is placed in an apparatus like the one shown in Figure 11.25, applying pressure greater than the osmotic pressure of the solution reverses the osmosis and pushes solvent molecules from the solution into the pure solvent. This technique of reverse osmosis is used for large-scale desalination of seawater and on smaller scales to produce high-purity tap water for drinking.
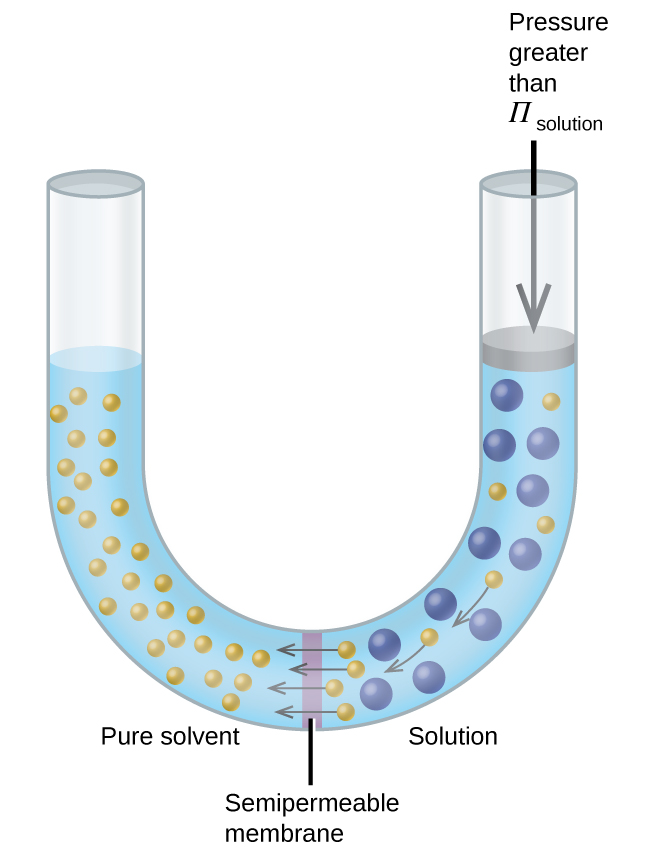
Chemistry in Everyday Life
Reverse Osmosis Water Purification
In the process of osmosis, diffusion serves to move water through a semipermeable membrane from a less concentrated solution to a more concentrated solution. Osmotic pressure is the amount of pressure that must be applied to the more concentrated solution to cause osmosis to stop. If greater pressure is applied, the water will go from the more concentrated solution to a less concentrated (more pure) solution. This is called reverse osmosis. Reverse osmosis (RO) is used to purify water in many applications, from desalination plants in coastal cities, to water-purifying machines in grocery stores (Figure 11.26), and smaller reverse-osmosis household units. With a hand-operated pump, small RO units can be used in third-world countries, disaster areas, and in lifeboats. Our military forces have a variety of generator-operated RO units that can be transported in vehicles to remote locations.

Examples of osmosis are evident in many biological systems because cells are surrounded by semipermeable membranes. Carrots and celery that have become limp because they have lost water can be made crisp again by placing them in water. Water moves into the carrot or celery cells by osmosis. A cucumber placed in a concentrated salt solution loses water by osmosis and absorbs some salt to become a pickle.
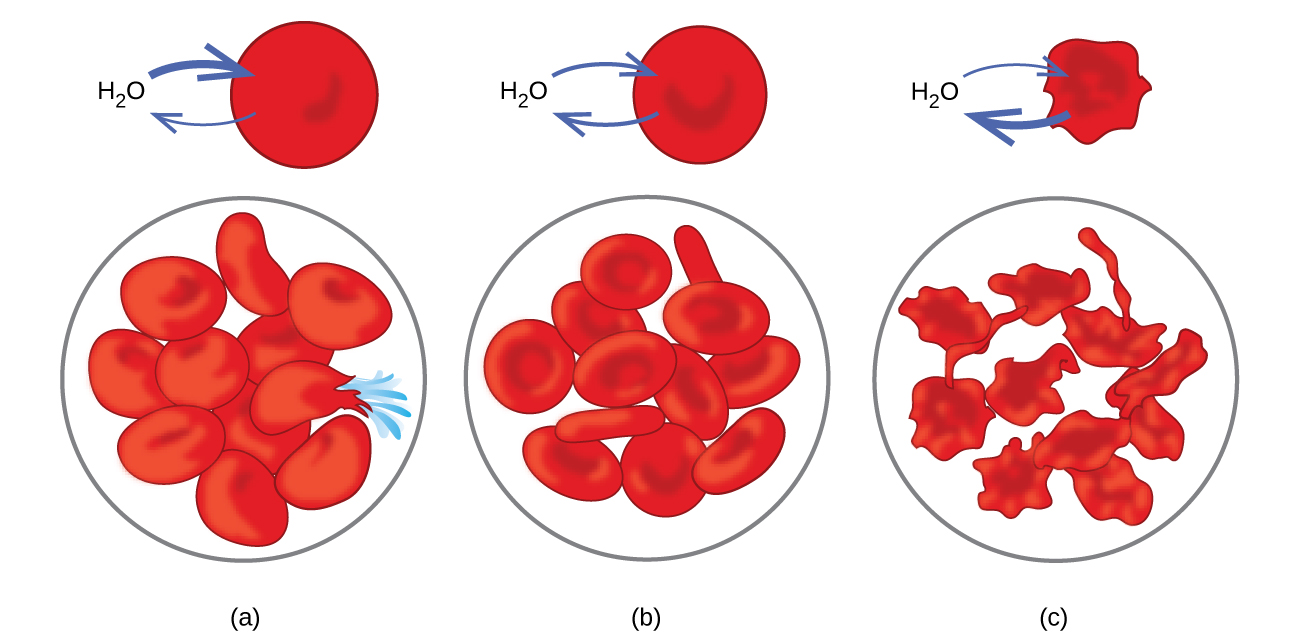
Osmosis can also affect animal cells. Solute concentrations are particularly important when solutions are injected into the body. Solutes in body cell fluids and blood serum give these solutions an osmotic pressure of approximately 7.7 atm. Solutions injected into the body must have the same osmotic pressure as blood serum; that is, they should be isotonic with blood serum. If a less concentrated solution, a hypotonic solution, is injected in sufficient quantity to dilute the blood serum, water from the diluted serum passes into the blood cells by osmosis, causing the cells to expand and rupture. This process is called hemolysis. When a more concentrated solution, a hypertonic solution, is injected, the cells lose water to the more concentrated solution, shrivel, and possibly die in a process called crenation. These effects are illustrated in Figure 11.27.