Chapter 11 Solutions and Colloids
11.6 Colligative Properties of Electrolyte Solutions
Learning Objectives
By the end of this section, you will be able to:
- Calculate the effect of the ionic dissociation on colligative properties
Colligative Properties of Electrolytes
As noted previously in this module, the colligative properties of a solution depend only on the number, not on the identity, of solute species dissolved. The concentration terms in the equations for various colligative properties (freezing point depression, boiling point elevation, osmotic pressure) pertain to all solute species present in the solution. For the solutions considered thus far in this chapter, the solutes have been nonelectrolytes that dissolve physically without dissociation or any other accompanying process. Each molecule that dissolves yields one dissolved solute molecule. The dissolution of an electrolyte, however, is not this simple, as illustrated by the two common examples below:
![]()
Considering the first of these examples, and assuming complete dissociation, a 1.0 m aqueous solution of NaCl contains 2.0 mole of ions (1.0 mol Na+ and 1.0 mol Cl−) per each kilogram of water, and its freezing point depression is expected to be:
When this solution is actually prepared and its freezing point depression measured, however, a value of 3.4°C is obtained. Similar discrepancies are observed for other ionic compounds, and the differences between the measured and expected colligative property values typically become more significant as solute concentrations increase. These observations suggest that the ions of sodium chloride (and other strong electrolytes) are not completely dissociated in solution.
To account for this and avoid the errors accompanying the assumption of total dissociation, an experimentally measured parameter named in honor of Nobel Prize-winning German chemist Jacobus Henricus van ’t Hoff is used. The van ’t Hoff factor (i) is defined as the ratio of solute particles in solution to the number of formula units dissolved:
|
Formula unit |
Classification |
Dissolution products |
i (predicted) |
i (measured) |
|---|---|---|---|---|
|
C12H22O11 (glucose) |
Nonelectrolyte |
C12H22O11 |
1 |
1.0 |
|
NaCl |
Strong electrolyte |
Na+, Cl− |
2 |
1.9 |
|
HCl |
Strong electrolyte (acid) |
H3O+, Cl− |
2 |
1.9 |
|
MgSO4 |
Strong electrolyte |
Mg2+, SO42− |
2 |
1.3 |
|
MgCl2 |
Strong electrolyte |
Mg2+, 2 Cl− |
3 |
2.7 |
|
FeCl3 |
Strong electrolyte |
Fe3+, 3 Cl− |
4 |
3.4 |
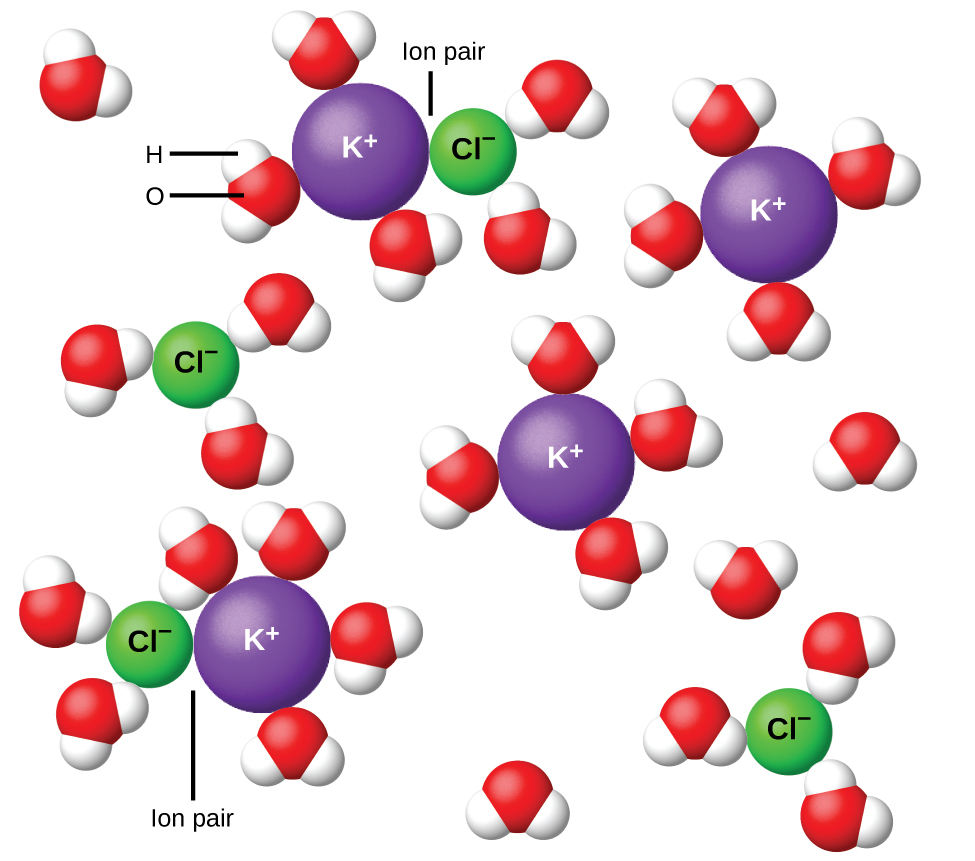
In 1923, the chemists Peter Debye and Erich Hückel proposed a theory to explain the apparent incomplete ionization of strong electrolytes. They suggested that although interionic attraction in an aqueous solution is very greatly reduced by solvation of the ions and the insulating action of the polar solvent, it is not completely nullified. The residual attractions prevent the ions from behaving as totally independent particles (Figure 11.28). In some cases, a positive and negative ion may actually touch, giving a solvated unit called an ion pair. Thus, the activity, or the effective concentration, of any particular kind of ion is less than that indicated by the actual concentration.
Ions become more and more widely separated the more dilute the solution, and the residual interionic attractions become less and less. Thus, in extremely dilute solutions, the effective concentrations of the ions (their activities) are essentially equal to the actual concentrations. Note that the van ’t Hoff factors for the electrolytes in Table 11.3 are for 0.05 m solutions, at which concentration the value of i for NaCl is 1.9, as opposed to an ideal value of 2.
Example 11.13 – The Freezing Point of a Solution of an Electrolyte
The concentration of ions in seawater is approximately the same as that in a solution containing 4.2 g of NaCl dissolved in 125 g of water. Use this information and a predicted value for the van ’t Hoff factor (Table 11.3) to determine the freezing temperature the solution (assume ideal solution behavior).
Solution
Solve this problem using the following series of steps. 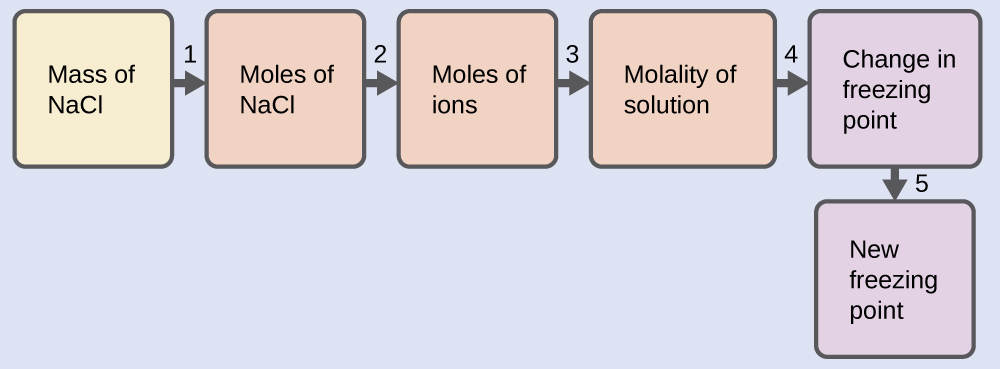
Step 1. Convert from grams to moles of NaCl using the molar mass of NaCl in the unit conversion factor.
Step 2. Determine the number of moles of ions present in the solution using the number of moles of ions in 1 mole of NaCl as the conversion factor (2 mol ions/1 mol NaCl).
Step 3. Determine the molality of the ions in the solution from the number of moles of ions and the mass of solvent, in kilograms.
Step 4. Use the direct proportionality between the change in freezing point and molal concentration to determine how much the freezing point changes.
Step 5. Determine the new freezing point from the freezing point of the pure solvent and the change.
Check Your Learning
Click here for a walkthrough of this problem!
First, we calculate the mols of CaCl2 and use the van ‘t Hoff factor (i) to calculate the mols of ions in solution:
Next, we calculate the molality of the solution:
Finally, we calculate the freezing point depression and the freezing point of the solution:
