11.7  Determining Molar Masses Using Colligative Properties

Nicole Bouvier-Brown; Saori Shiraki; J. Ryan Hunt; Emily Jarvis

Chapter 11 Solutions and Colloids

11.7 Determining Molar Masses Using Colligative Properties

Learning Objectives

By the end of this section, you will be able to:

Calculate the molar mass of a compound using experimentally determined colligative properties

Determination of Molar Masses

Osmotic pressure and changes in freezing point, boiling point, and vapor pressure are directly proportional to the number of solute species present in a given amount of solution. Consequently, measuring one of these properties for a solution prepared using a known mass of solute permits determination of the solute’s molar mass.

Example 11.11 – Determination of a Molar Mass from a Freezing Point Depression

A solution of 4.00 g of a nonelectrolyte dissolved in 55.0 g of benzene is found to freeze at 2.32°C. Assuming ideal solution behavior, what is the molar mass of this compound?

Solution

Solve this problem using the following steps.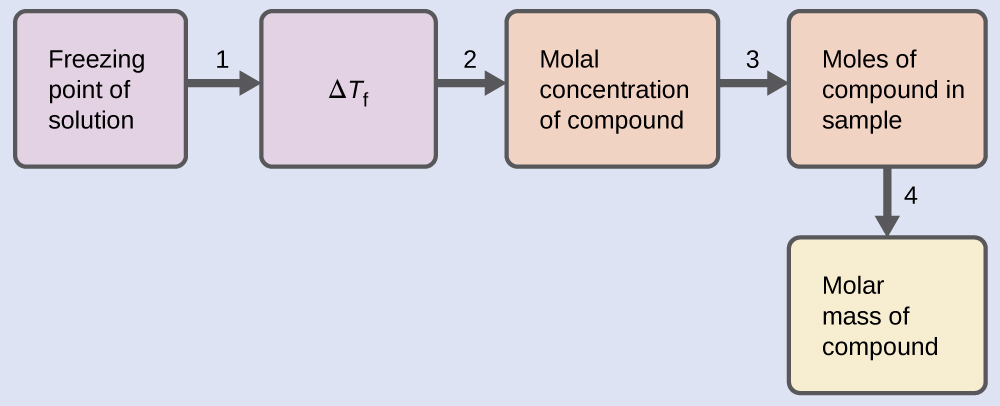

Step 1. Determine the change in freezing point from the observed freezing point and the freezing point of pure benzene (Table 11.2).

Δ T_{f} = {5.5}^{\circ} C - {2.32}^{\circ} C = {3.2}^{\circ} C

Step 2. Determine the molal concentration from K_f, the freezing point depression constant for benzene (Table 11.2), and ΔT_f.

Δ T_{f} = K_{f} m

m = \frac{Δ T_{f}}{K_{f}} = \frac{{3.2}^{\circ} C}{{5.12}^{\circ} C / m} = 0.63 m

Step 3. Determine the number of moles of compound in the solution from the molal concentration and the mass of solvent used to make the solution.

moles of solute = 0.0550 k g s o l v e n t (\frac{0.63 m o l s o l u t e}{1.00 k g s o l v e n t}) = 0.035 m o l s o l u t e

Step 4. Determine the molar mass from the mass of the solute and the number of moles in that mass.

molar mass = \frac{4.00 g}{0.035 m o l} = 1.1 \times 10^{2} g / m o l

Check Your Learning

Click here for a walkthrough of this problem!

We can find the boiling point (61.26 ^oC) and boiling point elevation constant (3.63 ^oC/m) in table 11.2. Then we can calculate the boiling point elevation:

Δ T_{b} = {64.5}^{\circ} C - {61.26}^{\circ} C = {3.2}^{\circ} C

Next, we can solve for the molality of the solution using the boiling point elevation constant:

Δ T_{b} = K_{b} m

m = \frac{Δ T_{b}}{K_{b}} = \frac{{3.2}^{\circ} C}{3.63 \frac{^{\circ} C}{m}} = 0.89 m

Next, we use the definition of molality and the mass of the solvent to solve for the mols of solute:

$mol of solute = 0.220 k g s o l v e n t (\frac{0.89 m o l}{1.00 k g s o l v e n t}) = 0.20 m o l$

Finally, we can calculate the molar mass using the provided mass of solute:

molar mass = \frac{35.7 g s o l u t e}{0.20 m o l s o l u t e} = 180 \frac{g}{m o l}

Example 11.12 – Determination of a Molar Mass from Osmotic Pressure

A 0.500 L sample of an aqueous solution containing 10.0 g of hemoglobin has an osmotic pressure of 5.9 torr at 22°C. Assuming ideal solution behavior, what is the molar mass of hemoglobin?

Solution

Here is one set of steps that can be used to solve the problem:

Step 1. Convert the osmotic pressure to atmospheres, then determine the molar concentration from the osmotic pressure.

Π = 5.9 t o r r (\frac{1 a t m}{760 t o r r}) = 7.8 \times 10^{- 3} a t m

Π = M R T

M = \frac{Π}{R T} = \frac{7.8 \times 10^{- 3} a t m}{(0.08206 \frac{L \cdot a t m}{m o l \cdot K}) (295 K)} = 3.2 \times 10^{- 4} M

Step 2. Determine the number of moles of hemoglobin in the solution from the concentration and the volume of the solution.

moles of hemoglobin = 0.500 L s o l n (\frac{3.2 \times 10^{- 4} m o l}{L s o l n}) = 1.6 \times 10^{- 4} m o l

Step 3. Determine the molar mass from the mass of hemoglobin and the number of moles in that mass.

molar mass = \frac{10.0 g}{1.6 \times 10^{- 4} m o l} = 6.2 \times 10^{4} g / m o l

Check Your Learning

Click here to see a walkthrough for this problem!

First, convert from torr to atm and then calculate the molarity of the solution:

Π = 0.56 t o r r (\frac{1 a t m}{760 t o r r}) = 7.37 \times 10^{- 4} a t m

$Π = M R T$

$M = \frac{Π}{R T} = \frac{7.37 \times 10^{- 4} a t m}{(0.08206 \frac{L \cdot a t m}{m o l \cdot K}) (298 K)} = 3.01 \times 10^{- 5} M$

Next, we can use the volume of the solution to calculate the mols of protein from the molarity:

mol of protein = 0.0250 L s o l u t i o n (\frac{3.01 \times 10^{- 5} m o l}{1.00 L s o l u t i o n}) = 7.53 \times 10^{- 7} m o l

Finally, we can calculate the molar mass of the protein:

$molar mass = \frac{0.02 g}{7.53 \times 10^{- 7} m o l} = 3 \times 10^{4} \frac{g}{m o l}$

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

11.7 Determining Molar Masses Using Colligative Properties Copyright © by Nicole Bouvier-Brown; Saori Shiraki; J. Ryan Hunt; and Emily Jarvis is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.