The rate laws discussed thus far relate the rate and the concentrations of reactants. We can also determine a second form of each rate law that relates the concentrations of reactants and time. These are called integrated rate laws. We can use an integrated rate law to determine the amount of reactant or product present after a period of time or to estimate the time required for a reaction to proceed to a certain extent. For example, an integrated rate law is used to determine the length of time a radioactive material must be stored for its radioactivity to decay to a safe level.

Using calculus, the differential rate law for a chemical reaction can be integrated with respect to time to give an equation that relates the amount of reactant or product present in a reaction mixture to the elapsed time of the reaction. This process can either be very straightforward or very complex, depending on the complexity of the differential rate law. For purposes of discussion, we will focus on the resulting integrated rate laws for first-, second-, and zero-order reactions.

First-Order Reactions

Integration of the rate law for a simple first-order reaction (rate = k[A]) results in an equation describing how the reactant concentration varies with time:

For mathematical convenience, this equation may be rearranged to other formats, including direct and indirect proportionalities:

In the next example exercise, a linear format for the integrated rate law will be convenient:

[latex]\ln [A]_t = (-k)(t) + \ln [A]_o[/latex]

[latex]y = mx + b[/latex]

A plot of ln[A]_t versus t for a first-order reaction is a straight line with a slope of −k and a y-intercept of ln[A]_o. If a set of rate data are plotted in this fashion but do not result in a straight line, the reaction is not first order in A.

Example 12.7 – Graphical Determination of Reaction Order and Rate Constant

Show that the data in Figure 12.2 can be represented by a first-order rate law by graphing ln[H₂O₂] versus time. Determine the rate constant for the decomposition of H₂O₂ from these data.

 

Solution

The data from Figure 12.2 are tabulated below, and a plot of ln[H₂O₂] is shown in Figure 12.9.

Time (h)	[H2O2] (M)	ln [H2O2]
0.00	1.000	0.000
6.00	0.500	−0.693
12.00	0.250	−1.386
18.00	0.125	−2.079
24.00	0.0625	−2.772

The plot of ln[H₂O₂] versus time is linear, indicating that the reaction may be described by a first-order rate law.

According to the linear format of the first-order integrated rate law, the rate constant is given by the negative of this plot’s slope.

[latex]slope = \frac {change \; in \; y}{change \; in \; x} = \frac {\Delta y}{\Delta x} = \frac {\Delta \ln [H_2O_2]}{\Delta t}[/latex]

[latex][/latex]

The slope of this line may be derived from two values of ln[H₂O₂] at different values of t (one near each end of the line is preferable). For example, the value of ln[H₂O₂] when t is 0.00 h is 0.000; the value when t = 24.00 h is −2.772

[latex]slope = \frac {-2.772 - 0.000}{24.00 \: h - 0.00 \: h} = \frac {-2.772}{24.00 \: h} = -0.116 \: h^{-1}[/latex]

[latex]k = - slope = - (-0.116 \: h^{-1}) = 0.116 \: h[/latex]

 

Check Your Learning

The following data for the reaction A → B+C  is plotted below.

Time (s)	[A] (M)
4.0	0.220
8.0	0.144
12.0	0.110
16.0	0.088
20.0	0.074

Second-Order Reactions

The equations that relate the concentrations of reactants and the rate constant of second-order reactions can be fairly complicated. To illustrate the point with minimal complexity, only the simplest second-order reactions will be described here, namely, those whose rates depend on the concentration of just one reactant. For these types of reactions, the differential rate law is written as:

For these second-order reactions, the integrated rate law is:

The integrated rate law for second-order reactions has the form of the equation of a straight line:

[latex]\frac {1}{[A]_t} = kt + \frac {1}{[A]_o}[/latex]

[latex]y = mx + b[/latex]

A plot of 1/[A]_t versus t for a second-order reaction is a straight line with a slope of k and a y-intercept of 1/[A]_o. If the plot is not a straight line, then the reaction is not second order.

Example 12.9 – Graphical Determination of Reaction Order and Rate Constant

The data below are for the same reaction described in Example 12.8. Prepare and compare two appropriate data plots to identify the reaction as being either first or second order. After identifying the reaction order, estimate a value for the rate constant.

 

Solution

Time (s)	[C4H6] (M)
0	1.00 × 10−2
1600	5.04 × 10−3
3200	3.37 × 10−3
4800	2.53 × 10−3
6200	2.08 × 10−3

In order to distinguish a first-order reaction from a second-order reaction, prepare a plot of ln [C₄H₆]_t versus t and compare it to a plot of 1/[C₄H₆]_t versus t. The values needed for these plots follow.

Time (s)	[latex]\frac {1}{[C_4H_6]}[/latex] (M−1)	ln [C4H6]
0	100	−4.605
1600	198	−5.289
3200	296	−5.692
4800	395	−5.978
6200	481	−6.175

The plots are shown in Figure 12.10, which clearly shows the plot of ln[C₄H₆]_t versus t is not linear, therefore the reaction is not first order. The plot of 1/[C₄H₆]_t versus t is linear, indicating that the reaction is second order.

.

According to the second-order integrated rate law, the rate constant is equal to the slope of the 1/[A]_t versus t plot. Using the data for t = 0 s and t = 6200 s, the rate constant is estimated as follows:

[latex]k = slope = \frac {481 \: M^{-1} \: - \: 100 \: M^{-1}}{6200 \: s \: - \: 0 \: s} = 0.0614 \: M^{-1} \cdot s^{-1}[/latex]

 

Check Your Learning

The following data is plotted below.

Time (s)	[A] (M)
5	0.952
10	0.625
15	0.465
20	0.370
25	0.308
35	0.230

Zero-Order Reactions

For zero-order reactions, the differential rate law is:

A zero-order reaction thus exhibits a constant reaction rate, regardless of the concentration of its reactant(s). This may seem counterintuitive, since the reaction rate certainly can’t be finite when the reactant concentration is zero. For purposes of this introductory text, it will suffice to note that zero-order kinetics are observed for some reactions only under certain specific conditions. These same reactions exhibit different kinetic behaviors when the specific conditions aren’t met, and for this reason the more prudent term pseudo-zero-order is sometimes used.

The integrated rate law for a zero-order reaction is a linear function:

[latex][A]_t = -kt + [A]_o[/latex]

[latex]y = mx + b[/latex]

A plot of [A] versus t for a zero-order reaction is a straight line with a slope of −k and a y-intercept of [A]₀. Figure 12.11 shows a plot of [NH₃] versus t for the thermal decomposition of ammonia at the surface of two different heated solids. The decomposition reaction exhibits first-order behavior at a quartz (SiO₂) surface, as suggested by the exponentially decaying plot of concentration versus time. On a tungsten surface, however, the plot is linear, indicating zero-order kinetics.

Example 12.10 – Graphical Determination of Zero-Order Rate Constant

Use the data plot in Figure 12.11 to graphically estimate the zero-order rate constant for ammonia decomposition at a tungsten surface.

.

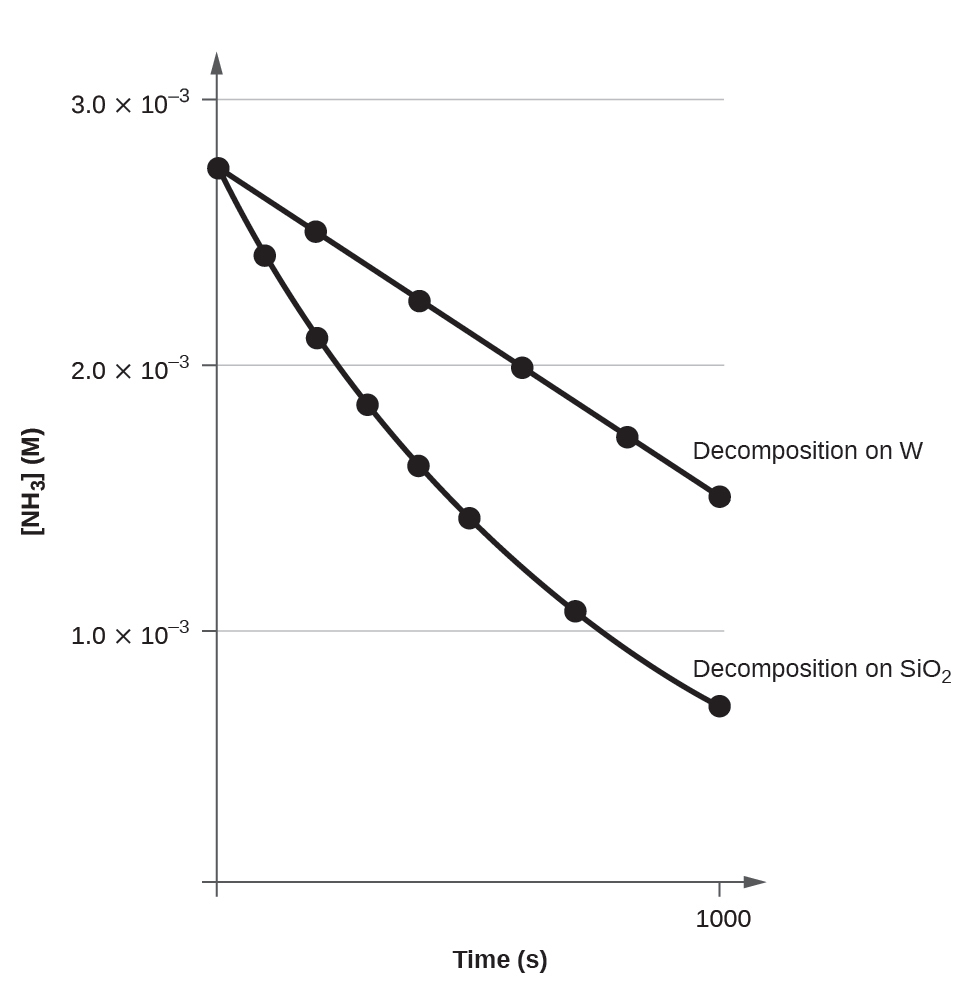
Solution

The integrated rate law for zero-order kinetics describes a linear plot of reactant concentration, [A]_t, versus time, t, with a slope equal to the negative of the rate constant, −k. Following the mathematical approach of previous examples, the slope of the linear data plot (for decomposition on W) is estimated from the graph. Using the ammonia concentrations at t = 0 and t = 1000 s:

[latex]k = -slope = \frac {0.0015 \: mol/L \: - \: 0.0028 \: mol/L}{1000 \: s \: - \: 0 \: s} = 1.3 \times 10^{-6} \: \frac{mol}{L \cdot s}[/latex]

 

Check Your Learning

Click here for a walkthrough of this problem!

The zero-order integrated rate law is

[latex][A]_t = -kt + [A]_o[/latex]

We can straightforwardly solve for t using k from the example above:

[latex]-kt\ =\left[A\right]_t-\left[A\right]_0[/latex]

[latex]t\ =-\frac{\left[A\right]_t-\left[A\right]_0}{k}=-\frac{0.0001\ \frac{\text{mol}}{L}-0.0028\ \frac{\text{mol}}{L}}{1.36\ \times10^{-6}\ \frac{\text{mol}}{L\ \cdot s}}=2080\ s\ \left(\frac{1\ \min}{60\ s}\right)=35\ \min[/latex]

The Half-Life of a Reaction

The half-life of a reaction (t _1/2) is the time required for one-half of a given amount of reactant to be consumed. In each succeeding half-life, half of the remaining concentration of the reactant is consumed. Using the decomposition of hydrogen peroxide (Figure 12.2) as an example, we find that during the first half-life (from 0.00 hours to 6.00 hours), the concentration of H₂O₂ decreases from 1.000 M to 0.500 M. During the second half-life (from 6.00 hours to 12.00 hours), it decreases from 0.500 M to 0.250 M; during the third half-life, it decreases from 0.250 M to 0.125 M. The concentration of H₂O₂ decreases by half during each successive period of 6.00 hours. The decomposition of hydrogen peroxide is a first-order reaction, and, as can be shown, the half-life of a first-order reaction is independent of the concentration of the reactant. However, half-lives of reactions with other orders depend on the concentrations of the reactants.

First-Order Reactions

An equation relating the half-life of a first-order reaction to its rate constant may be derived from the integrated rate law as follows:

[latex]\ln {\frac {[A]_o}{[A]_t}} = kt[/latex]

[latex]t = \ln {\frac {[A]_o}{[A]_t}} \cdot \frac {1}{k}[/latex]

Invoking the definition of half-life, symbolized t _1/2, requires that the concentration of A at this point is one-half its initial concentration: t = t _1/2, [A]_t = [latex]\frac {1}{2}[/latex][A]_o.

Substituting these terms into the rearranged integrated rate law and simplifying yields the equation for half-life:

[latex]t_{1/2} = \ln {\frac {[A]_o}{\frac {1}{2} [A]_o}} \cdot \frac {1}{k} = \ln 2 \cdot \frac {1}{k} = \frac {0.693}{k}[/latex]

This equation describes an expected inverse relation between the half-life of the reaction and its rate constant, k. Faster reactions exhibit larger rate constants and correspondingly shorter half-lives. Slower reactions exhibit smaller rate constants and longer half-lives.

Example 12.11 – Calculation of a First-order Rate Constant using Half-Life

Calculate the rate constant for the first-order decomposition of hydrogen peroxide in water at 40°C, using the data given in Figure 12.12.

.

Solution

Inspecting the concentration/time data in Figure 12.12 shows the half-life for the decomposition of H₂O₂ is 2.16 × 10⁴ s:

[latex]t_{1/2} = \frac {0.693}{k}[/latex]

[latex]k = \frac {0.693}{t_{1/2}} = \frac {0.693}{2.16 \times 10^4 \: s} = 3.21 \times 10^{-5} \: s^{-1}[/latex]

 

Check Your Learning

Click here to see the math!

[latex]t_{1/2} = \frac {0.693}{k}=\frac{0.693}{0.138 \: d^{-1}}=5.02 \: d[/latex]

Second-Order Reactions

Following the same approach as used for first-order reactions, an equation relating the half-life of a second-order reaction to its rate constant and initial concentration may be derived from its integrated rate law:

Restrict t to t _1/2

[latex]\frac {1}{\frac {1}{2}[A]_o} - \frac {1}{[A]_o} = \frac {2}{[A]_o} - \frac {1}{[A]_o} = \frac {1}{[A]_o} = kt_{1/2}[/latex]

[latex]t_{1/2} = \frac {1}{k[A]_o}[/latex]

For a second-order reaction, t _1/2 is inversely proportional to the concentration of the reactant, and the half-life increases as the reaction proceeds because the concentration of reactant decreases. Unlike with first-order reactions, the rate constant of a second-order reaction cannot be calculated directly from the half-life unless the initial concentration is known.

Zero-Order Reactions

As for other reaction orders, an equation for zero-order half-life may be derived from the integrated rate law:

Restricting the time and concentrations to those defined by half-life: t = t _1/2 and [A]_t = [latex]\frac {1}{2}[/latex][A]_o. Substituting these terms into the zero-order integrated rate law yields:

[latex]\frac {[A]_o}{2} = -k \: t_{1/2} + [A]_o[/latex]

[latex]k \: t_{1/2} = \frac {[A]_o}{2}[/latex]

[latex]t_{1/2} = \frac {[A]_o}{2k}[/latex]

As for all reaction orders, the half-life for a zero-order reaction is inversely proportional to its rate constant. However, the half-life of a zero-order reaction increases as the initial concentration increases.

Equations for both differential and integrated rate laws and the corresponding half-lives for zero-, first-, and second-order reactions are summarized in Table 12.2.