15.1  Solubility Product

Nicole Bouvier-Brown; Saori Shiraki; J. Ryan Hunt; Emily Jarvis

Chapter 15 Equilibria of Other Reaction Classes

15.1 Solubility Product

Learning Objectives

By the end of this section, you will be able to:

Write chemical equations and equilibrium expressions representing solubility equilibria
Calculate the solubility of compounds using the solubility product

Solubility equilibria are established when the dissolution and precipitation of a solute species occur at equal rates. These equilibria underlie many natural and technological processes, ranging from tooth decay to water purification. An understanding of the factors affecting compound solubility is, therefore, essential to the effective management of these processes. This section applies previously introduced equilibrium concepts and tools to systems involving dissolution and precipitation.

The Solubility Product

Chapter 11.3 on solutions discussed that the solubility of a substance can vary from essentially zero (insoluble or sparingly soluble) to infinity (miscible). A solute with finite solubility can yield a saturated solution when it is added to a solvent in an amount exceeding its solubility, resulting in a heterogeneous mixture of the saturated solution and the excess, undissolved solute. For example, a saturated solution of silver chloride is one in which the equilibrium shown below has been established.

[latex][/latex]

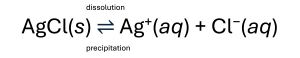
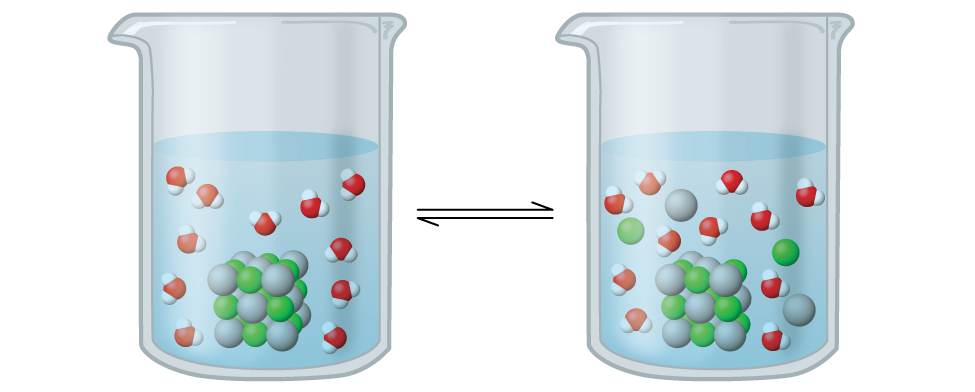
In this solution, an excess of solid AgCl dissolves and dissociates to produce aqueous Ag⁺ and Cl^– ions at the same rate that these aqueous ions combine and precipitate to form solid AgCl (Figure 15.2). Because silver chloride is a sparingly soluble salt, the equilibrium concentration of its dissolved ions in the solution is relatively low.

.

**Figure 15.2** Silver chloride is a sparingly soluble ionic solid. When it is added to water, it dissolves slightly and produces a mixture consisting of a very dilute solution of Ag⁺ and Cl^– ions in equilibrium with undissolved silver chloride.

The equilibrium constant for solubility equilibria such as this one is called the solubility product constant, K_sp, in this case

[latex][/latex]

AgCl(s) ⇌ Ag⁺(aq) + Cl⁻(aq) [latex]K_{sp} = [Ag^+(aq)] \, [Cl^-(aq)][/latex]

Recall that only gases and solutes are represented in equilibrium constant expressions, so the K_sp does not include a term for the undissolved AgCl. A listing of solubility product constants for several sparingly soluble compounds is provided in Appendix J.

Example 15.1 – Writing Equations and Solubility Products

Write the dissolution equation and the solubility product expression for each of the following slightly soluble ionic compounds:

(a) AgI, silver iodide, a solid with antiseptic properties

(b) CaCO₃, calcium carbonate, the active ingredient in many over-the-counter chewable antacids

(c) Mg(OH)₂, magnesium hydroxide, the active ingredient in Milk of Magnesia

(d) Mg(NH₄)PO₄, magnesium ammonium phosphate, an essentially insoluble substance used in tests for magnesium

(e) Ca₅(PO₄)₃OH, the mineral apatite, a source of phosphate for fertilizers

Solution

(a) AgI(s) ⇌ Ag⁺(aq) + I⁻(aq) [latex]K_{sp} = [Ag^+] \, [I^-][/latex]

(b) CaCO₃(s) ⇌ Ca²⁺(aq) + CO₃²⁻(aq) [latex]K_{sp} = [Ca^{2+}] \, [CO_3^{2-}][/latex]

(c) Mg(OH)₂(s) ⇌ Mg²⁺(aq) + 2 OH⁻(aq) [latex]K_{sp} = [Mg^{2+}] \, [OH^-]^2[/latex]

(d) Mg(NH₄)PO₄(s) ⇌ Mg²⁺(aq) + NH₄+(aq) + PO₄³⁻(aq)

[latex]K_{sp} = [Mg^{2+}] \, [NH_4^+] \, [PO_4^{3-}][/latex]

(e) Ca₅(PO₄)₃OH(s) ⇌ 5 Ca²⁺(aq) + 3 PO₄³⁻(aq) + OH⁻(aq)

[latex]K_{sp} = [Ca^{2+}]^5 \, [PO_4^{3-}]^3 \, [OH^-][/latex]

Check Your Learning

Click here to see the dissolution equations and solubility products for these compounds.

(1) BaSO₄(s) ⇌ Ba²⁺(aq) + SO₄²⁻(aq) [latex]K_{sp} = [Ba^{2+}] \, [SO_4^{2-}][/latex]
(2) Ag₂SO₄(s) ⇌ 2 Ag⁺(aq) + SO₄²⁻(aq) [latex]K_{sp} = [Ag^+]^2 \, [SO_4^{2-}][/latex]
(3) Al(OH)₃(s) ⇌ Al³⁺(aq) + 3 OH⁻(aq) [latex]K_{sp} = [Al^{3+}] \, [OH^-]^3[/latex]
(4) Pb(OH)Cl(s) ⇌ Pb²⁺(aq) + OH⁻(aq) + Cl⁻(aq) [latex]K_{sp} = [Pb^{2+}] \, [OH^-] \, [Cl^-][/latex]

K_sp and Solubility

The K_sp of a slightly soluble ionic compound may be simply related to its measured solubility provided the dissolution process involves only dissociation and solvation, for example:

M_pX_q(s) ⇌ p M^m+(aq) + q Xⁿ⁻(aq)

For cases such as these, one may derive K_sp values from provided solubilities, or vice-versa. Calculations of this sort are most conveniently performed using a compound’s molar solubility, measured as moles of dissolved solute per liter, in other words in molarity, of saturated solution.

Example 15.2 – Calculation of K_sp from Equilibrium Concentrations

Fluorite, CaF₂, is a slightly soluble solid that dissolves according to the equation:

CaF₂(s) ⇌ Ca²⁺(aq) + 2 F⁻(aq)

The concentration of Ca²⁺ in a saturated solution of CaF₂ is 2.15 × 10^–4 M. What is the solubility product of fluorite?

Solution

According to the stoichiometry of the dissolution equation, the fluoride ion molarity of a CaF₂ solution is equal to twice its calcium ion molarity:

[latex][F^-] = 2.15 \times 10^{-4} \: \frac {mol \: Ca^{2+}}{L} \: \left( \frac {2 \: mol \: F^-}{1 \: mol \: Ca^{2+}} \right) = 4.30 \times 10^{-4} \: M \: F^-[/latex]

[latex][/latex]

Substituting the ion concentrations into the K_sp expression gives

[latex][/latex]

[latex]K_{sp} = [Ca^{2+}] \, [F^-]^2 = (2.15 \times 10^{-4}) \, (4.30 \times 10^{-4})^2 = 3.98 \times 10^{-11}[/latex]

Check Your Learning

Click here for the solution!

According to the stoichiometry of the dissolution equation

[latex][OH^-] = 1.31 \times 10^{-4} \: \frac {mol \: Mg^{2+}}{L} \: \left( \frac {2 \: mol \: OH^-}{1 \: mol \: Mg^{2+}} \right) = 2.62 \times 10^{-4} \: M[/latex]

[latex][/latex]

Substituting the ion concentrations into the K_sp expression gives

[latex][/latex]

[latex]K_{sp} = [Mg^{2+}] \, [OH^-]^2 = (1.31 \times 10^{-4}) \, (2.62 \times 10^{-4})^2 = 8.99 \times 10^{-12}[/latex]

Example 15.3 – Determination of Molar Solubility from K_sp

The K_sp of copper(I) bromide, CuBr, is 6.3 × 10^–9.

Calculate the molar solubility of copper bromide.

Solution

The dissolution equation and solubility product expression are

CuBr(s) ⇌ Cu+(aq) + Br−(aq) [latex]K_{sp} = [Cu^+] \, [Br^-][/latex]

[latex][/latex]

Following the ICE approach to this calculation yields the table

	CuBr(s)	⇌	Cu⁺(aq)	+	Br⁻(aq)
I (M)	—		0		0
C (M)	(−x)		+x		+x
E (M)	—		x		x

Substituting the equilibrium concentration terms into the solubility product expression and solving for x yields

[latex]K_{sp} = [Cu^+] \, [Br^-][/latex]

[latex][/latex]

[latex]6.3 \times 10^{-9} = x \cdot x = x^2[/latex]

[latex][/latex]

[latex]x = \sqrt {6.3 \times 10^{-9}} = 7.9 \times 10^{-5}[/latex]

[latex][/latex]

Since the dissolution stoichiometry shows one mole of copper(I) ion and one mole of bromide ion are produced for each moles of CuBr dissolved, the molar solubility of CuBr is 7.9 × 10^–5 M.

Check Your Learning

Click here for a walkthrough!

The dissolution equation and solubility product expression are

AgI(s) ⇌ Ag⁺ (aq) + I^– (aq) [latex]K_{sp} = [Ag^+] \, [I^-][/latex]

[latex][/latex]

Following the ICE approach to this calculation yields the table

	AgI(s)	⇌	Ag⁺ (aq)	+	I^– (aq)
I (M)	—		0		0
C (M)	(−x)		+x		+x
E (M)	—		x		x

Substituting the equilibrium concentration terms into the solubility product expression and solving for x yields

[latex]1.5 \times 10^{-16} = x^2[/latex]

[latex][/latex]

[latex]x = \sqrt {1.5 \times 10^{-16}} = 1.2 \times 10^{-8}[/latex]

[latex][/latex]

Since the dissolution stoichiometry shows one mole of silver ion and one mole of iodide ion are produced for each mole of AgI dissolved, the molar solubility of AgI is 1.2 × 10^–8 M.

Example 15.4 – Determination of Molar Solubility from K_sp

The K_sp of calcium hydroxide, Ca(OH)₂, is 1.3 × 10^–6.

Calculate the molar solubility of calcium hydroxide.

Solution

The dissolution equation and solubility product expression are

Ca(OH)₂(s) ⇌ Ca²⁺(aq) + 2 OH⁻(aq) [latex]K_{sp} = [Ca^{2+}] \, [OH^-]^2[/latex]

[latex][/latex]

The ICE table for this system is

	Ca(OH)₂(s)	⇌	Cu²⁺(aq)	+	2 OH⁻(aq)
I (M)	—		0		0
C (M)	(−x)		+x		+2x
E (M)	—		x		2x

Substituting terms for the equilibrium concentrations into the solubility product expression and solving for x gives

[latex]K_{sp} = [Ca^{2+}] \, [OH^-]^2[/latex]

[latex][/latex]

[latex]1.3 \times 10^{-6} = x \, (2x)^2 = x \, (4x^2) = 4x^3[/latex]

[latex][/latex]

[latex]x = \sqrt [3]{\frac {1.3 \times 10^{-6}}{4}} = \sqrt [3]{3.3 \times 10^{-7}} = 6.9 \times 10^{-3}[/latex]

[latex][/latex]

As defined in the ICE table, x is the molarity of calcium ion in the saturated solution. The dissolution stoichiometry shows a 1:1 relation between moles of calcium ion in solution and moles of compound dissolved, and so, the molar solubility of Ca(OH)₂ is 6.9 × 10^–3 M.

Check Your Learning

Click here for a walkthrough!

The dissolution equation and solubility product expression are

PbI₂ (s) ⇌ Pb²⁺(aq) + 2 I⁻(aq) [latex]K_{sp} = [Pb^{2+}] \, [I^-]^2[/latex]

[latex][/latex]

The ICE table for this system is

	PbI₂ (s)	⇌	Pb²⁺(aq)	+	2 I⁻(aq)
I (M)	—		0		0
C (M)	(−x)		+x		+2x
E (M)	—		x		2x

Substituting terms for the equilibrium concentrations into the solubility product expression and solving for x gives

[latex]1.4 \times 10^{-8} = x \, (2x)^2 = x \, (4x^2) = 4x^3[/latex]

[latex][/latex]

[latex]x = \sqrt [3]{\frac {1.4 \times 10^{-8}}{4}} = 1.5 \times 10^{-3}[/latex]

[latex][/latex]

As defined in the ICE table, x is the molarity of lead ion in the saturated solution. The dissolution stoichiometry shows a 1:1 relation between moles of lead ion in solution and moles of compound dissolved, so the molar solubility of PbI₂ is 1.5 × 10^–3 M.

Example 15.5 – Determination of K_sp from Gram Solubility

Many of the pigments used by artists in oil-based paints (Figure 15.3) are sparingly soluble in water. For example, the solubility of the artist’s pigment chrome yellow, PbCrO₄, is 4.6 × 10^–6 g/L.

Determine the solubility product for PbCrO₄.

.

**Figure 15.3** Oil paints contain pigments that are very slightly soluble in water. In addition to chrome yellow (PbCrO₄), examples include Prussian blue (Fe₇(CN)₁₈), the reddish-orange color vermilion (HgS), and green color veridian (Cr₂O₃). (credit: Sonny Abesamis)

Solution

Before calculating the solubility product, the provided solubility must be converted to molar solubility:

[latex][PbCrO_4] = \frac {4.6 \times 10^{-6} \cancel {g \: PbCrO_4}}{1 \: L} \: \left( \frac {1 \: mol \: PbCrO_4}{323.2 \cancel {g \: PbCrO_4}} \right) = 1.4 \times 10^{-8} \: M \: PbCrO_4[/latex]

The dissolution equation for this compound is

PbCrO₄(s) ⇌ Pb²⁺(aq) + CrO₄²⁻(aq)

[latex][/latex]

The dissolution stoichiometry shows a 1:1 relation between the molar amounts of compound and its two ions, and so both [Pb²⁺] and [CrO₄²⁻] are equal to the molar solubility of PbCrO₄:

[Pb²⁺] = [CrO₄²⁻] = 1.4 × 10⁻⁸ M

[latex][/latex]

[latex]K_{sp} = [Pb^{2+}] \, [CrO_4^{2-}] = (1.4 \times 10^{-8}) \, (1.4 \times 10^{-8}) = 2.0 \times 10^{-16}[/latex]

Check Your Learning

Click here for a walkthrough!

Before calculating the solubility product, the provided solubility must be converted to molar solubility:

[latex][TlCl] = \frac {3.12 \cancel {g \: PbCrO_4}}{1 \: L} \: \left( \frac {1 \: mol \: TlCl}{239.82 \cancel {g \: TlCl}} \right) = 0.0130 \: M[/latex]

The dissolution equation for this compound is

TlCl(s) ⇌ Tl⁺ (aq) + Cl^– (aq)

[latex][/latex]

The dissolution stoichiometry shows a 1:1 relation between the molar amounts of compound and its two ions, and so both [Tl⁺] and [Cl^–] are equal to the molar solubility of TlCl:

[latex][/latex]

[Tl⁺] = [Cl^–] = 0.0130 M

[latex][/latex]

[latex]K_{sp} = [Tl^+] \, [Cl^-] = (0.0130) \, (0.0130) = 1.69 \times 10^{-4}[/latex]

Example 15.6 – Calculating the Solubility of Hg₂Cl₂

Calomel, Hg₂Cl₂, is a compound composed of the diatomic ion of mercury(I), Hg₂²⁺, and chloride ions, Cl^–. Although most mercury compounds are now known to be poisonous, eighteenth-century physicians used calomel as a medication. Their patients rarely suffered any mercury poisoning from the treatments because calomel has a very low solubility, as suggested by its very small K_sp:

Hg₂Cl₂(s) ⇌ Hg₂²⁺(aq) + 2 Cl⁻(aq) K_sp = 1.1 × 10⁻¹⁸

[latex][/latex]

Calculate the molar solubility of Hg₂Cl₂.

Solution

The dissolution stoichiometry shows a 1:1 relation between the amount of compound dissolved and the amount of mercury (I) ions, and so the molar solubility of Hg₂Cl₂ is equal to the concentration of Hg₂²⁺ions.

Following the ICE approach results in

	Hg₂Cl₂(s)	⇌	Hg₂²⁺(aq)	+	2 Cl⁻(aq)
I (M)	—		0		0
C (M)	(−x)		+x		+2x
E (M)	—		x		2x

Substituting the equilibrium concentration terms into the solubility product expression and solving for x gives

[latex]K_{sp} = [Hg_2^{2+}] \, [Cl^-]^2[/latex]

[latex][/latex]

[latex]1.1 \times 10^{-18} = x \, (2x)^2 = 4x^3[/latex]

[latex][/latex]

[latex]x = \sqrt [3]{\frac {1.1 \times 10^{-18}}{4}} = 6.5 \times 10^{-7}[/latex]

[latex][/latex]

[latex][Hg_2^{2+}] = x = 6.5 \times 10^{-7} \: M[/latex]

[latex][/latex]

[latex][Cl^-] = 2x = 2 \, (6.5 \times 10^{-7}) = 1.3 \times 10^{-6} \: M[/latex]

[latex][/latex]

The dissolution stoichiometry shows the molar solubility of Hg₂Cl₂ is equal to [Hg₂²⁺], or 6.5 × 10^–7 M.

Check Your Learning

Click here for a walkthrough!

Following the ICE approach results in

	MgF₂ (s)	⇌	Mg²⁺ (aq)	+	2 F^– (aq)
I (M)	—		0		0
C (M)	(−x)		+x		+2x
E (M)	—		x		2x

Substituting the equilibrium concentration terms into the solubility product expression and solving for x gives

[latex]K_{sp} = [Mg^{2+}] \, [F^-]^2[/latex]

[latex][/latex]

[latex]6.4 \times 10^{-9} = x \, (2x)^2 = 4x^3[/latex]

[latex][/latex]

[latex]x = [Mg^{2+}] = \sqrt [3] {\frac {6.4 \times 10^{-9}}{4}} = 1.2 \times 10^{-3}[/latex]

[latex][/latex]

The dissolution stoichiometry shows a 1:1 relation between the amount of compound dissolved and the amount of Mg²⁺ ions, and so the molar solubility of MgF₂ is equal to 1.2 × 10^–3 M.

How Sciences Interconnect

Using Barium Sulfate for Medical Imaging

**Figure 15.4** A suspension of barium sulfate coats the intestinal tract, permitting greater visual detail than a traditional X-ray. (credit modification of work by “glitzy queen00”/Wikimedia Commons)

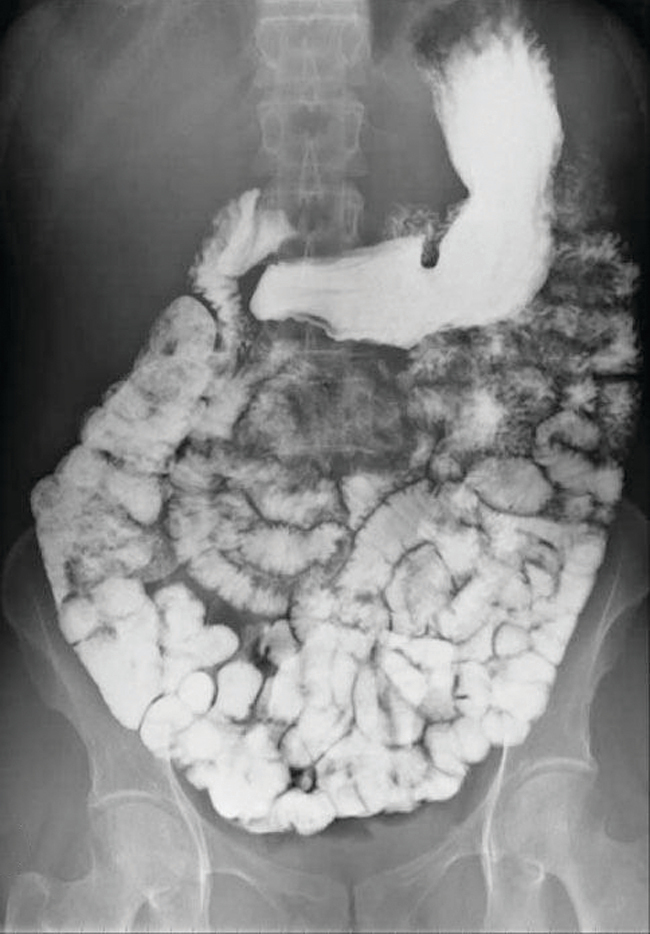
Various types of medical imaging techniques are used to aid diagnoses of illnesses in a noninvasive manner. One such technique utilizes the ingestion of a barium compound before taking an X-ray image. A suspension of barium sulfate, a chalky powder, is ingested by the patient. Since the K_sp of barium sulfate is 2.3 × 10^–8, very little of it dissolves as it coats the lining of the patient’s intestinal tract. Barium-coated areas of the digestive tract then appear on an X-ray as white, allowing for greater visual detail than a traditional X-ray (Figure 15.4).

Medical imaging using barium sulfate can be used to diagnose acid reflux disease, Crohn’s disease, and ulcers in addition to other conditions.

Visit this website for more information on how barium is used in medical diagnoses and which conditions it is used to diagnose.

Media Attributions

dissolution and precipitation