Chapter 16 Thermodynamics
16.6 Free Energy and Equilibrium
Learning Objectives
By the end of this section, you will be able to:
- Explain how free energy is related to equilibrium
- Calculate the equilibrium constant for a reaction using its Gibbs free energy change (or vice versa)
The free energy change for a process may be viewed as a measure of its “driving force”:
- A negative value for ΔG represents a driving force for the process in the forward direction
- A positive value for ΔG represents a driving force for the process in the reverse direction.
- When ΔG is zero, the forward and reverse driving forces are equal, and the process occurs in both directions at the same rate (the system is at equilibrium).
In the chapter on equilibrium the reaction quotient, Q, was introduced as a convenient measure of the status of an equilibrium system. Recall that Q is the numerical value of the mass action expression for the system, and that you may use its value to identify the direction in which a reaction will proceed in order to achieve equilibrium. When Q is lesser than the equilibrium constant, K, the reaction will proceed in the forward direction until equilibrium is reached and Q = K. Conversely, if Q > K, the process will proceed in the reverse direction until equilibrium is achieved.
The free energy change for a process taking place with reactants and products present under nonstandard conditions (pressures other than 1 bar; concentrations other than 1 M) is related to the standard free energy change according to this equation:
[latex]\Delta G = \Delta G^o + RT \ln Q[/latex]
R is the gas constant (8.314 J/K mol), T is the kelvin or absolute temperature, and Q is the reaction quotient. For gas phase equilibria, the pressure-based reaction quotient, QP, is used. The concentration-based reaction quotient, QC, is used for condensed phase equilibria. This equation may be used to predict the spontaneity for a process under any given set of conditions as illustrated in Example 16.12.
2 NH3(g) → 3 H2(g) + N2(g) ΔG° = 33.0kJ/mol
What is the free energy change for the reaction above under the specified conditions?
T = 25°C, PN2 = 0.870atm, PH2 = 0.250atm, and PNH3 = 12.9atm
Solution
First, we can calculate the reaction quotient (QP) for the reaction:
[latex]Q_P = \frac{P_{H_2}^3 \ P_{N_2}}{P_{NH_3}^2} = \frac{(0.250)^3 \ (0.870)}{12.9^2} = 8.17 \times 10^{-5}[/latex]
The equation relating free energy change to standard free energy change and reaction quotient may be used directly:
[latex]\Delta G = \Delta G^o + RT \ln Q[/latex]
[latex]= 33.0 \frac{kJ}{mol} + (8.3145 \ \frac{J}{mol \cdot K} \times 298 \ K \times \ln (8.17 \times 10^{-5}))[/latex]
[latex]= 9680 \ \frac{J}{mol} = 9.68 \ \frac{kJ}{mol}[/latex]
Since the computed value for ΔG is positive, the reaction is nonspontaneous under these conditions.
Check Your Learning
Click here for a walkthrough of these problems!
The ideal gas law can be used to calculate the partial pressure of each gas:
[latex]P = \frac{nRT}{V} = \frac{(0.1 \ mol)(0.0821 \frac{L \ atm}{mol \ K})(1148 \ K)}{5 \ L} = 1.88 atm[/latex]
We can then straightforwardly calculate QP:
[latex]Q_P = \frac{P_{H_2}^3 \ P_{N_2}}{P_{NH_3}^2} = \frac{(1.88)^3 \ (1.88)}{1.88^2} = 3.55[/latex]
Then we can calculate ΔG under these conditions:
[latex]\Delta G = \Delta G^o + RT \ln Q[/latex]
[latex]= 33.0 \frac{kJ}{mol} + (8.3145 \ \frac{J}{mol \cdot K} \times 1148 \ K \times \ln (3.55))[/latex]
[latex]= 45000 \ \frac{J}{mol} = 45.0 \ \frac{kJ}{mol}[/latex]
ΔG is positive under these conditions, so the reaction is nonspontaneous.
Because this is a larger positive number than the one calculated above (9.68 kJ/mol), the reaction is less spontaneous under these conditions.
For a system at equilibrium, Q = K and ΔG = 0, and the previous equation may be written as
[latex]\Delta G = 0 = \Delta G^o + RT \ln K[/latex] (at equilibrium)
This form of the equation provides a useful link between these two essential thermodynamic properties (K and ΔG°), and it can be used to derive equilibrium constants from standard free energy changes and vice versa. The relations between standard free energy changes and equilibrium constants are summarized in Table 16.4.
|
K |
ΔG° |
Composition of an Equilibrium Mixture |
|
> 1 |
< 0 |
Products are more abundant |
|
< 1 |
> 0 |
Reactants are more abundant |
|
= 1 |
= 0 |
Reactants and products are comparably abundant |
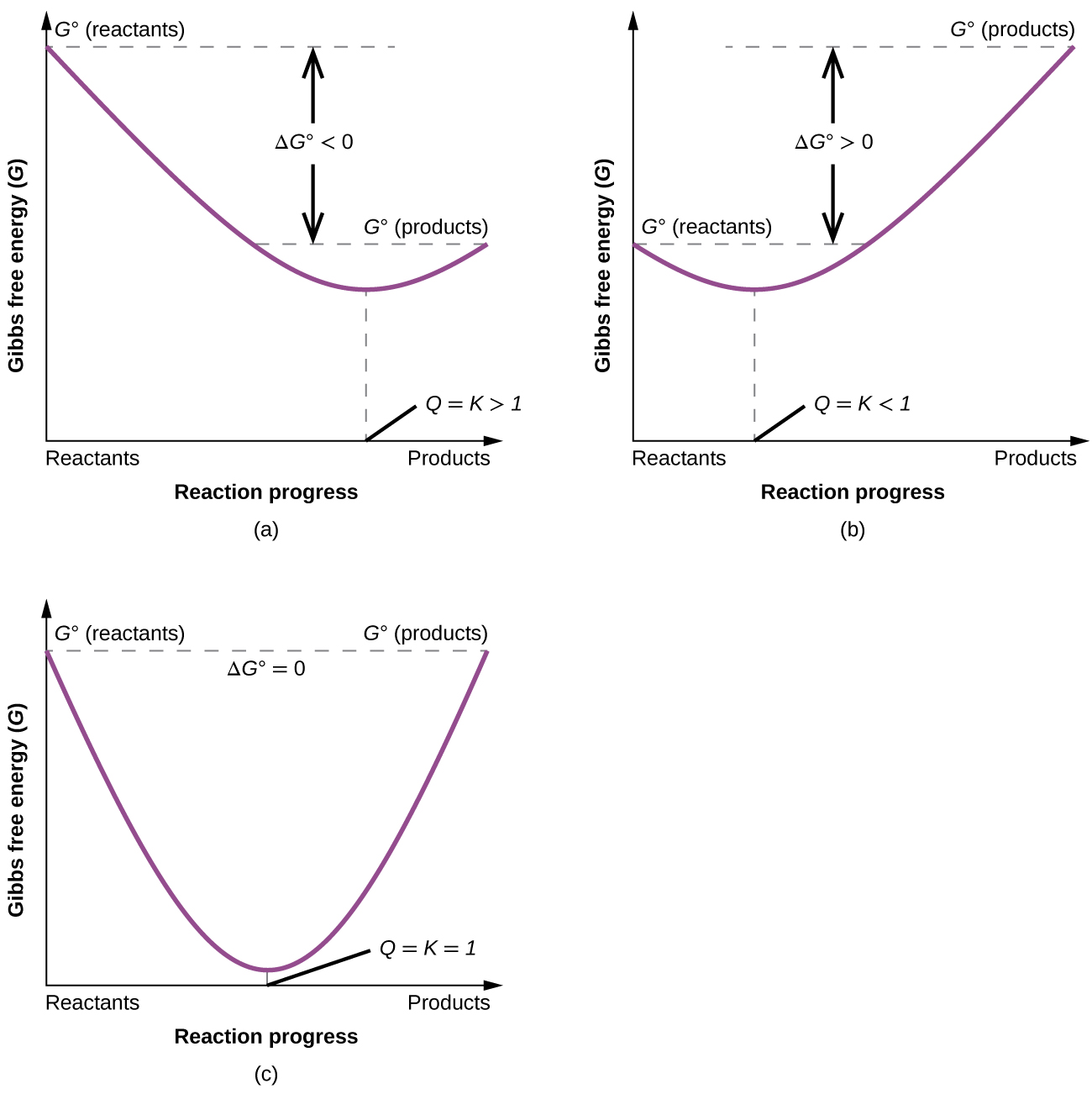
To further illustrate the relation between these two essential thermodynamic concepts, consider the observation that reactions spontaneously proceed in a direction that ultimately establishes equilibrium. As may be shown by plotting the free energy versus the extent of the reaction (for example, as reflected in the value of Q), equilibrium is established when the system’s free energy is minimized (Figure 16.14). If a system consists of reactants and products in nonequilibrium amounts (Q ≠ K), the reaction will proceed spontaneously in the direction necessary to establish equilibrium.
Example 16.13 – Calculating an Equilibrium Constant using Standard Free Energy Change
Given that the standard free energies of formation of Ag+(aq), Cl−(aq), and AgCl(s) are 77.1 kJ/mol, −131.2 kJ/mol, and −109.8 kJ/mol, respectively, calculate the solubility product, Ksp, for AgCl.
Solution
The reaction of interest is the following:
The standard free energy change for this reaction is first computed using standard free energies of formation for its reactants and products:
[latex]\Delta G^o =\left(1\right)\Delta G_f^o\ \left(Ag^+(aq)\right)+\left(1\right)\Delta G_f^o\left(Cl^-(aq)\right)-\left(1\right)\Delta G_f^o\left(AgCl(s)\right)[/latex]
[latex]=\left(1\right)\left(77.1\ \frac{kJ}{mol}\right)+\left(1\right)\left(-131.2\ \frac{kJ}{mol} \right)-\left(1\right)\left(-109.8\ \frac{kJ}{mol}\right)=55.7\ \frac{kJ}{mol}[/latex]
The equilibrium constant for the reaction under standard conditions (298.15 K) may then be derived from its standard free energy change:
[latex]K_{sp} = e^{- \frac{\Delta G^o}{RT}} = e^{- \frac{55700 \frac{J}{mol} }{(8.3145 \frac{J}{mol \cdot K})(298.15 K)}} = 1.74 \times 10^{-10}[/latex]
This result is in reasonable agreement with the value provided in Appendix J.
Check Your Learning
Use the thermodynamic data provided in Appendix G to calculate the equilibrium constant for the dissociation of dinitrogen tetroxide at 25°C.
Click here for a walkthrough and the answer!
First, we calculate ΔGo for the reaction:
[latex]\Delta G^o =\left(1\right)\Delta G_f^o\ \left(N_2O_4\right)-\left(2\right)\Delta G_f^o\left(NO_2\right)[/latex]
[latex]=\left(1\right)\left(99.8\ \frac{kJ}{mol}\right)-\left(2\right)\left(51.30\ \frac{kJ}{mol}\right)=-2.80\ \frac{kJ}{mol}[/latex]
Then we can calculate K:
[latex]K= e^{- \frac{\Delta G^o}{RT}} = e^{- \frac{-2800 \frac{J}{mol} }{(8.3145 \frac{J}{mol \cdot K})(298.15 K)}} = 3.1[/latex]
