Chapter 1 Essential Ideas
Chapter 1 Problems
1.1 Chemistry in Context
1.1. Explain how you could experimentally determine whether the outside temperature is higher or lower than 0°C (32°F) without using a thermometer.
1.2. Identify each of the following statements as being most similar to a hypothesis, a law, or a theory. Explain your reasoning.
(a) Falling barometric pressure precedes the onset of bad weather.
(b) All life on earth has evolved from a common, primitive organism through the process of natural selection.
(c) My truck’s gas mileage has dropped significantly, probably because it’s due for a tune-up.
1.3. Identify each of the following statements as being most similar to a hypothesis, a law, or a theory. Explain your reasoning.
(a) The pressure of a sample of gas is directly proportional to the temperature of the gas.
(b) Matter consists of tiny particles that can combine in specific ratios to form substances with specific properties.
(c) At a higher temperature, solids (such as salt or sugar) will dissolve better in water.
1.4. Identify each of the underlined items as a part of either the macroscopic domain, the microscopic domain, or the symbolic domain of chemistry. For any in the symbolic domain, indicate whether they are symbols for a macroscopic or a microscopic feature.
(a) The mass of a lead pipe is 14 lb.
(b) The mass of a certain chlorine atom is 35 amu.
(c) A bottle with a label that reads Al contains aluminum metal.
(d) Al is the symbol for an aluminum atom.
1.5. Identify each of the underlined items as a part of either the macroscopic domain, the microscopic domain, or the symbolic domain of chemistry. For those in the symbolic domain, indicate whether they are symbols for a macroscopic or a microscopic feature.
(a) A certain molecule contains one H atom and one Cl atom.
(b) Copper wire has a density of about 8 g/cm3.
(c) The bottle contains 15 grams of Ni powder.
(d) A sulfur molecule is composed of eight sulfur atoms.
1.6. According to one theory, the pressure of a gas increases as its volume decreases because the molecules in the gas have to move a shorter distance to hit the walls of the container. Does this theory follow a macroscopic or microscopic description of chemical behavior? Explain your answer.
1.7. The amount of heat required to melt 2 lbs of ice is twice the amount of heat required to melt 1 lb of ice. Is this observation a macroscopic or microscopic description of chemical behavior? Explain your answer.
1.2 Phases and Classification of Matter
1.8. Why is an object’s mass, rather than its weight, used to indicate the amount of matter it contains?
1.9. What properties distinguish solids from liquids? Liquids from gases? Solids from gases?
1.10. How does a heterogeneous mixture differ from a homogeneous mixture? How are they similar?
1.11. How does a homogeneous mixture differ from a pure substance? How are they similar?
1.12. How does an element differ from a compound? How are they similar?
1.13. How do molecules of elements and molecules of compounds differ? In what ways are they similar?
1.14. How does an atom differ from a molecule? In what ways are they similar?
1.15. Many of the items you purchase are mixtures of pure compounds. Select three of these commercial products and prepare a list of the ingredients that are pure compounds.
1.16. Classify each of the following as an element, a compound, or a mixture:
(a) copper
(b) water
(c) nitrogen
(d) sulfur
(e) air
(f) sucrose
(g) a substance composed of molecules each of which contains two iodine atoms
(h) gasoline
1.17. Classify each of the following as an element, a compound, or a mixture:
(a) iron
(b) oxygen
(c) mercury oxide
(d) pancake syrup
(e) carbon dioxide
(f) a substance composed of molecules each of which contains one hydrogen atom and one chlorine atom
(g) baking soda
(h) baking powder
1.18. A sulfur atom and a sulfur molecule are not identical. What is the difference?
1.19. How are the molecules in oxygen gas, the molecules in hydrogen gas, and water molecules similar? How do they differ?
1.20. Why are astronauts in space said to be “weightless,” but not “massless”?
1.21. Prepare a list of the principal chemicals consumed and produced during the operation of an automobile.
1.22. Matter is everywhere around us. Make a list by name of fifteen different kinds of matter that you encounter every day. Your list should include (and label at least one example of each) the following: a solid, a liquid, a gas, an element, a compound, a homogenous mixture, a heterogeneous mixture, and a pure substance.
1.23. When elemental iron corrodes it combines with oxygen in the air to ultimately form red brown iron(III) oxide called rust. (a) If a shiny iron nail with an initial mass of 23.2 g is weighed after being coated in a layer of rust, would you expect the mass to have increased, decreased, or remained the same? Explain. (b) If the mass of the iron nail increases to 24.1 g, what mass of oxygen combined with the iron?
1.24. As stated in the text, convincing examples that demonstrate the law of conservation of matter outside of the laboratory are few and far between. Indicate whether the mass would increase, decrease, or stay the same for the following scenarios where chemical reactions take place:
(a) Exactly one pound of bread dough is placed in a baking tin. The dough is cooked in an oven at 350°F releasing a wonderful aroma of freshly baked bread during the cooking process. Is the mass of the baked loaf less than, greater than, or the same as the one pound of original dough? Explain.
(b) When magnesium burns in air a white flaky ash of magnesium oxide is produced. Is the mass of magnesium oxide less than, greater than, or the same as the original piece of magnesium? Explain.
(c) Antoine Lavoisier, the French scientist credited with first stating the law of conservation of matter, heated a mixture of tin and air in a sealed flask to produce tin oxide. Did the mass of the sealed flask and contents decrease, increase, or remain the same after the heating?
1.25. Yeast converts glucose to ethanol and carbon dioxide during anaerobic fermentation as depicted in the simple chemical equation here:
glucose → ethanol + carbon dioxide
(a) If 200.0 g of glucose is fully converted, what will be the total mass of ethanol and carbon dioxide produced?
(b) If the fermentation is carried out in an open container, would you expect the mass of the container and contents after fermentation to be less than, greater than, or the same as the mass of the container and contents before fermentation? Explain.
(c) If 97.7 g of carbon dioxide is produced, what mass of ethanol is produced?
1.3 Physical and Chemical Properties
1.26. Classify the six underlined properties in the following paragraph as chemical or physical:
Fluorine is a pale yellow gas that reacts with most substances. The free element melts at −220°C and boils at −188°C. Finely divided metals burn in fluorine with a bright flame. Nineteen grams of fluorine will react with 1.0 gram of hydrogen.
1.27. Classify each of the following changes as physical or chemical:
(a) condensation of steam
(b) burning of gasoline
(c) souring of milk
(d) dissolving of sugar in water
(e) melting of gold
1.28. Classify each of the following changes as physical or chemical:
(a) coal burning
(b) ice melting
(c) mixing chocolate syrup with milk
(d) explosion of a firecracker
(e) magnetizing of a screwdriver
1.29. The volume of a sample of oxygen gas changed from 10 mL to 11 mL as the temperature changed. Is this a chemical or physical change?
1.30. A 2.0-liter volume of hydrogen gas combined with 1.0 liter of oxygen gas to produce 2.0 liters of water vapor. Does oxygen undergo a chemical or physical change?
1.31. Explain the difference between extensive properties and intensive properties.
1.32. Identify the following properties as either extensive or intensive.
(a) volume
(b) temperature
(c) humidity
(d) heat
(e) boiling point
1.33. The density (d) of a substance is an intensive property that is defined as the ratio of its mass (m) to its volume (V).
Considering that mass and volume are both extensive properties, explain why their ratio, density, is intensive.
1.4 Measurements
1.34. Is one liter about an ounce, a pint, a quart, or a gallon?
1.35. Is a meter about an inch, a foot, a yard, or a mile?
1.36. Indicate the SI base units or derived units that are appropriate for the following measurements:
(a) the length of a marathon race (26 miles 385 yards)
(b) the mass of an automobile
(c) the volume of a swimming pool
(d) the speed of an airplane
(e) the density of gold
(f) the area of a football field
(g) the maximum temperature at the South Pole on April 1, 1913
1.37. Indicate the SI base units or derived units that are appropriate for the following measurements:
(a) the mass of the moon
(b) the distance from Dallas to Oklahoma City
(c) the speed of sound
(d) the density of air
(e) the temperature at which alcohol boils
(f) the area of the state of Delaware
(g) the volume of a flu shot or a measles vaccination
1.38. Give the name and symbol of the prefixes used with SI units to indicate multiplication by the following exact quantities.
(a) 103
(b) 10−2
(c) 0.1
(d) 10−3
(e) 1,000,000
(f) 0.000001
1.39. Give the name of the prefix and the quantity indicated by the following symbols that are used with SI base units.
(a) c
(b) d
(c) G
(d) k
(e) m
(f) n
(g) p
(h) T
1.40. A large piece of jewelry has a mass of 132.6 g. A graduated cylinder initially contains 48.6 mL water. When the jewelry is submerged in the graduated cylinder, the total volume increases to 61.2 mL.
(a) Determine the density of this piece of jewelry.
(b) Assuming that the jewelry is made from only one substance, what substance is it likely to be? Explain.
1.41. Visit this density simulation and click the “turn fluid into water” button to adjust the density of liquid in the beaker to 1.00 g/mL.
(a) Use the water displacement approach to measure the mass and volume of the unknown material (select the green block with question marks).
(b) Use the measured mass and volume data from step (a) to calculate the density of the unknown material.
(c) Link out to the link provided.
(d) Assuming this material is a copper-containing gemstone, identify its three most likely identities by comparing the measured density to the values tabulated at this gemstone density guide.
(e) How are mass and density related for blocks of the same volume?
1.42. Visit this density simulation and click the “reset” button to ensure all simulator parameters are at their default values.
(a) Use the water displacement approach to measure the mass and volume of the red block.
(b) Use the measured mass and volume data from step (a) to calculate the density of the red block.
(c) Use the vertical green slide control to adjust the fluid density to values well above, then well below, and finally nearly equal to the density of the red block, reporting your observations.
1.43. Visit this density simulation and click the “turn fluid into water” button to adjust the density of liquid in the beaker to 1.00 g/mL. Change the block material to foam, and then wait patiently until the foam block stops bobbing up and down in the water.
(a) The foam block should be floating on the surface of the water (that is, only partially submerged). What is the volume of water displaced?
(b) Use the water volume from part (a) and the density of water (1.00 g/mL) to calculate the mass of water displaced.
(c) Remove and weigh the foam block. How does the block’s mass compare to the mass of displaced water from part (b)?
1.5 Measurement Uncertainty, Accuracy, and Precision
1.44. Express each of the following numbers in scientific notation with correct significant figures:
(a) 711.0
(b) 0.239
(c) 90743
(d) 134.2
(e) 0.05499
(f) 10000.0
(g) 0.000000738592
1.45. Express each of the following numbers in exponential notation with correct significant figures:
(a) 704
(b) 0.03344
(c) 547.9
(d) 22086
(e) 1000.00
(f) 0.0000000651
(g) 0.007157
1.46. Indicate whether each of the following can be determined exactly or must be measured with some degree of uncertainty:
(a) the number of eggs in a basket
(b) the mass of a dozen eggs
(c) the number of gallons of gasoline necessary to fill an automobile gas tank
(d) the number of cm in 2 m
(e) the mass of a textbook
(f) the time required to drive from San Francisco to Kansas City at an average speed of 53 mi/h
1.47. Indicate whether each of the following can be determined exactly or must be measured with some degree of uncertainty:
(a) the number of seconds in an hour
(b) the number of pages in this book
(c) the number of grams in your weight
(d) the number of grams in 3 kilograms
(e) the volume of water you drink in one day
(f) the distance from San Francisco to Kansas City
1.48. How many significant figures are contained in each of the following measurements?
(a) 38.7 g
(b) 2 × 1018 m
(c) 3,486,002 kg
(d) 9.74150 × 10−4 J
(e) 0.0613 cm3
(f) 17.0 kg
(g) 0.01400 g/mL
1.49. How many significant figures are contained in each of the following measurements?
(a) 53 cm
(b) 2.05 × 108 m
(c) 86,002 J
(d) 9.740 × 104 m/s
(e) 10.0613 m3
(f) 0.17 g/mL
(g) 0.88400 s
1.50. The following quantities were reported on the labels of commercial products. Determine the number of significant figures in each.
(a) 0.0055 g active ingredients
(b) 12 tablets
(c) 3% hydrogen peroxide
(d) 5.5 ounces
(e) 473 mL
(f) 1.75% bismuth
(g) 0.001% phosphoric acid
(h) 99.80% inert ingredients
1.51. Round off each of the following numbers to two significant figures:
(a) 0.436
(b) 9.000
(c) 27.2
(d) 135
(e) 1.497 × 10−3
(f) 0.445
1.52. Round off each of the following numbers to two significant figures:
(a) 517
(b) 86.3
(c) 6.382 × 103
(d) 5.0008
(e) 22.497
(f) 0.885
1.53. Perform the following calculations and report each answer with the correct number of significant figures.
(a) 628 × 342
(b) (5.63 × 102) × (7.4 × 103)
(c) 28.013.483
(d) 8119 × 0.000023
(e) 14.98 + 27,340 + 84.7593
(f) 42.7 + 0.259
1.54. Perform the following calculations and report each answer with the correct number of significant figures.
(a) 62.8 × 34
(b) 0.147 + 0.0066 + 0.012
(c) 38 × 95 × 1.792
(d) 15 – 0.15 – 0.6155
(e) 8.78 × 0.05000.478
(f) 140 + 7.68 + 0.014
(g) 28.7 – 0.0483
(h) (88.5−87.57)45.13
1.55. Consider the results of the archery contest shown in this figure.
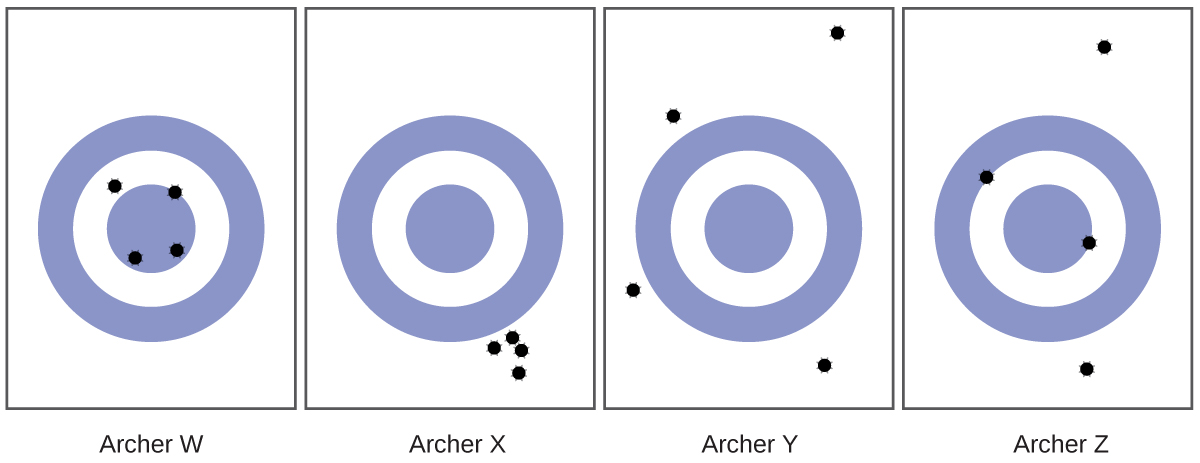
(a) Which archer is most precise?
(b) Which archer is most accurate?
(c) Who is both least precise and least accurate?
1.56. Classify the following sets of measurements as accurate, precise, both, or neither.
(a) Checking for consistency in the weight of chocolate chip cookies: 17.27 g, 13.05 g, 19.46 g, 16.92 g
(b) Testing the volume of a batch of 25-mL pipettes: 27.02 mL, 26.99 mL, 26.97 mL, 27.01 mL
(c) Determining the purity of gold: 99.9999%, 99.9998%, 99.9998%, 99.9999%
1.6 Mathematical Treatment of Measurement Results
1.57. Write conversion factors (as ratios) for the number of:
(a) yards in 1 meter
(b) liters in 1 liquid quart
(c) pounds in 1 kilogram
1.58. Write conversion factors (as ratios) for the number of:
(a) kilometers in 1 mile
(b) liters in 1 cubic foot
(c) grams in 1 ounce
1.59. The label on a soft drink bottle gives the volume in two units: 2.0 L and 67.6 fl oz. Use this information to derive a conversion factor between the English and metric units. How many significant figures can you justify in your conversion factor?
1.60. The label on a box of cereal gives the mass of cereal in two units: 978 grams and 34.5 oz. Use this information to find a conversion factor between the English and metric units. How many significant figures can you justify in your conversion factor?
1.61. Soccer is played with a round ball having a circumference between 27 and 28 in. and a weight between 14 and 16 oz. What are these specifications in units of centimeters and grams?
1.62. A woman’s basketball has a circumference between 28.5 and 29.0 inches and a maximum weight of 20 ounces (two significant figures). What are these specifications in units of centimeters and grams?
1.63. How many milliliters of a soft drink are contained in a 12.0-oz can?
1.64. A barrel of oil is exactly 42 gal. How many liters of oil are in a barrel?
1.65. The diameter of a red blood cell is about 3 × 10−4 in. What is its diameter in centimeters?
1.66. The distance between the centers of the two oxygen atoms in an oxygen molecule is 1.21 × 10−8 cm. What is this distance in inches?
1.67. Is a 197-lb weight lifter light enough to compete in a class limited to those weighing 90 kg or less?
1.68. A very good 197-lb weight lifter lifted 192 kg in a move called the clean and jerk. What was the mass of the weight lifted in pounds?
1.69. Many medical laboratory tests are run using 5.0 μL blood serum. What is this volume in milliliters?
1.70. If an aspirin tablet contains 325 mg aspirin, how many grams of aspirin does it contain?
1.71. Use scientific (exponential) notation to express the following quantities in terms of the SI base units in Table 1.2:
(a) 0.13 g
(b) 232 Gg
(c) 5.23 pm
(d) 86.3 mg
(e) 37.6 cm
(f) 54 μm
(g) 1 Ts
(h) 27 ps
(i) 0.15 mK
1.72. Complete the following conversions between SI units.
(a) 612 g = ________ mg
(b) 8.160 m = ________ cm
(c) 3779 μg = ________ g
(d) 781 mL = ________ L
(e) 4.18 kg = ________ g
(f) 27.8 m = ________ km
(g) 0.13 mL = ________ L
(h) 1738 km = ________ m
(i) 1.9 Gg = ________ g
1.73. Gasoline is sold by the liter in many countries. How many liters are required to fill a 12.0-gal gas tank?
1.74. Milk is sold by the liter in many countries. What is the volume of exactly 1/2 gal of milk in liters?
1.75. A long ton is defined as exactly 2240 lb. What is this mass in kilograms?
1.76. Make the conversion indicated in each of the following:
(a) the men’s world record long jump, 29 ft 4¼ in., to meters
(b) the greatest depth of the ocean, about 6.5 mi, to kilometers
(c) the area of the state of Oregon, 96,981 mi2, to square kilometers
(d) the volume of 1 gill (exactly 4 oz) to milliliters
(e) the estimated volume of the oceans, 330,000,000 mi3, to cubic kilometers.
(f) the mass of a 3525-lb car to kilograms
(g) the mass of a 2.3-oz egg to grams
1.77. Make the conversion indicated in each of the following:
(a) the length of a soccer field, 120 m (three significant figures), to feet
(b) the height of Mt. Kilimanjaro, at 19,565 ft, the highest mountain in Africa, to kilometers
(c) the area of an 8.5- × 11-inch sheet of paper in cm2
(d) the displacement volume of an automobile engine, 161 in.3, to liters
(e) the estimated mass of the atmosphere, 5.6 × 1015 tons, to kilograms
(f) the mass of a bushel of rye, 32.0 lb, to kilograms
(g) the mass of a 5.00-grain aspirin tablet to milligrams (1 grain = 0.00229 oz)
1.78. Many chemistry conferences have held a 50-Trillion Angstrom Run (two significant figures). How long is this run in kilometers and in miles? (1 Å = 1 × 10−10 m)
1.79. A chemist’s 50-Trillion Angstrom Run (see Problem 1.78) would be an archeologist’s 10,900 cubit run. How long is one cubit in meters and in feet? (1 Å = 1 × 10−8 cm)
1.80. The gas tank of a certain luxury automobile holds 22.3 gallons according to the owner’s manual. If the density of gasoline is 0.8206 g/mL, determine the mass in kilograms and pounds of the fuel in a full tank.
1.81. As an instructor is preparing for an experiment, he requires 225 g phosphoric acid. The only container readily available is a 150-mL Erlenmeyer flask. Is it large enough to contain the acid, whose density is 1.83 g/mL?
1.82. To prepare for a laboratory period, a student lab assistant needs 125 g of a compound. A bottle containing 1/4 lb is available. Did the student have enough of the compound?
1.83. A chemistry student is 159 cm tall and weighs 45.8 kg. What is her height in inches and weight in pounds?
1.84. In a recent Grand Prix, the winner completed the race with an average speed of 229.8 km/h. What was his speed in miles per hour, meters per second, and feet per second?
1.85. Solve these problems about lumber dimensions.
(a) To describe to a European how houses are constructed in the US, the dimensions of “two-by-four” lumber must be converted into metric units. The thickness × width × length dimensions are 1.50 in. × 3.50 in. × 8.00 ft in the US. What are the dimensions in cm × cm × m?
(b) This lumber can be used as vertical studs, which are typically placed 16.0 in. apart. What is that distance in centimeters?
1.86. The mercury content of a stream was believed to be above the minimum considered safe—1 part per billion (ppb) by weight. An analysis indicated that the concentration was 0.68 parts per billion. What quantity of mercury in grams was present in 15.0 L of the water, the density of which is 0.998 g/ml?
1.87. Calculate the density of aluminum if 27.6 cm3 has a mass of 74.6 g.
1.88. Osmium is one of the densest elements known. What is its density if 2.72 g has a volume of 0.121 cm3?
1.89. Calculate these masses.
(a) What is the mass of 6.00 cm3 of mercury, density = 13.5939 g/cm3?
(b) What is the mass of 25.0 mL octane, density = 0.702 g/cm3?
1.90. Calculate these masses.
(a) What is the mass of 4.00 cm3 of sodium, density = 0.97 g/cm3 ?
(b) What is the mass of 125 mL gaseous chlorine, density = 3.16 g/L?
1.91. Calculate these volumes.
(a) What is the volume of 25 g iodine, density = 4.93 g/cm3?
(b) What is the volume of 3.28 g gaseous hydrogen, density = 0.089 g/L?
1.92. Calculate these volumes.
(a) What is the volume of 11.3 g graphite, density = 2.25 g/cm3?
(b) What is the volume of 39.657 g bromine, density = 2.928 g/cm3?
1.93. Convert the boiling temperature of gold, 2966°C, into degrees Fahrenheit and kelvin.
1.94. Convert the temperature of scalding water, 54°C, into degrees Fahrenheit and kelvin.
1.95. Convert the temperature of the coldest area in a freezer, −10°F, to degrees Celsius and kelvin.
1.96. Convert the temperature of dry ice, −77°C, into degrees Fahrenheit and kelvin.
1.97. Convert the boiling temperature of liquid ammonia, −28.1°F, into degrees Celsius and kelvin.
1.98. The label on a pressurized can of spray disinfectant warns against heating the can above 130°F. What are the corresponding temperatures on the Celsius and kelvin temperature scales?
1.99. The weather in Europe was unusually warm during the summer of 1995. The TV news reported temperatures as high as 45°C. What was the temperature on the Fahrenheit scale?