4.2  Reaction Stoichiometry

Nicole Bouvier-Brown; Saori Shiraki; J. Ryan Hunt; Emily Jarvis

Chapter 4 Stoichiometry of Chemical Reactions

4.2 Reaction Stoichiometry

Learning Objectives

By the end of this section, you will be able to:

Explain the concept of stoichiometry as it pertains to chemical reactions
Use balanced chemical equations to derive stoichiometric factors relating amounts of reactants and products
Perform stoichiometric calculations involving mass, moles, and solution molarity

A balanced chemical equation provides a great deal of information in a very succinct format. Chemical formulas provide the identities of the reactants and products involved in the chemical change, allowing classification of the reaction. Coefficients provide the relative numbers of these chemical species, allowing a quantitative assessment of the relationships between the amounts of substances consumed and produced by the reaction. These quantitative relationships are known as the reaction’s stoichiometry, a term derived from the Greek words stoicheion (meaning “element”) and metron (meaning “measure”). In this module, the use of balanced chemical equations for various stoichiometric applications is explored.

The general approach to using stoichiometric relationships is similar in concept to the way people go about many common activities. Food preparation, for example, offers an appropriate comparison. A recipe for making eight pancakes calls for 1 cup pancake mix, 3/4 cup milk, and one egg. The “equation” representing the preparation of pancakes per this recipe is

1 cup mix + 3/4 cup milk + 1 egg → 8 pancakes

If two dozen pancakes are needed for a big family breakfast, the ingredient amounts must be increased proportionally according to the amounts given in the recipe. For example, the number of eggs required to make 24 pancakes is

24 p a n c a k e s \frac{1 e g g}{8 p a n c a k e s} = 3 e g g s

Balanced chemical equations are used in much the same fashion to determine the amount of one reactant required to react with a given amount of another reactant, or to yield a given amount of product, and so forth. The coefficients in the balanced equation are used to derive stoichiometric factors that permit computation of the desired quantity. To illustrate this idea, consider the production of ammonia by reaction of hydrogen and nitrogen:

N₂(g) + 3 H₂(g) → 2 NH₃(g)

This equation shows ammonia molecules are produced from hydrogen molecules in a 2:3 ratio, and stoichiometric factors may be derived using any amount (number) unit:

\frac{2 N H_{3} m o l e c u l e s}{3 H_{2} m o l e c u l e s} o r \frac{2 d o z N H_{3} m o l e c u l e s}{3 d o z H_{2} m o l e c u l e s} o r \frac{2 m o l N H_{3} m o l e c u l e s}{3 H_{2} m o l m o l e c u l e s}

These stoichiometric factors can be used to compute the number of ammonia molecules produced from a given number of hydrogen molecules, or the number of hydrogen molecules required to produce a given number of ammonia molecules. Similar factors may be derived for any pair of substances in any chemical equation.

Example 4.3 – Moles of Reactant Required in a Reaction

How many moles of I₂ are required to react with 0.429 mol of Al according to the following equation (see Figure 4.4)?

2 Al + 3 I₂ → 2 AlI₃

_.

**Figure 4.4** Aluminum and iodine react to produce aluminum iodide. The heat of the reaction vaporizes some of the solid iodine as a purple vapor. (credit: modification of work by Mark Ott)

Solution

Referring to the balanced chemical equation, the stoichiometric factor relating the two substances of interest is [latex]\frac {3 \: mol \: I_2}{2 \: mol \: Al}[/latex]. The molar amount of iodine is derived by multiplying the provided molar amount of aluminum by this factor:

$m o l I_{2} = 0.429 m o l A l \frac{3 m o l I_{2}}{2 m o l A l} = 0.644 m o l I_{2}$

Check Your Learning

Example 4.4 – Number of Product Molecules Generated by a Reaction

How many carbon dioxide molecules are produced when 0.75 mol of propane is combusted according to this equation?

C₃H₈ + 5 O₂ → 3 CO₂ + 4 H₂O

Solution

The approach here is the same as for the previous example, though the absolute number of molecules is requested, not the number of moles of molecules. This will simply require use of the moles-to-numbers conversion factor, Avogadro’s number.

The balanced equation shows that carbon dioxide is produced from propane in a 3:1 ratio:

\frac{3 m o l C O_{2}}{1 m o l C_{3} H_{8}}

Using this stoichiometric factor, the provided molar amount of propane, and Avogadro’s number,

[latex]0.75 \cancel {mol \: C_3H_8} \; \frac {3 \cancel {mol \: CO_2}}{1 \cancel {mol \: C_3H_8}} \; \frac {6.022 \times 10^{23} \: CO_2 \: molecules}{\cancel {mol \: CO_2}} = 1.4 \times 10^{24} \; CO_2 \; molecules[/latex]

Check Your Learning

These examples illustrate the ease with which the amounts of substances involved in a chemical reaction of known stoichiometry may be related. Directly measuring numbers of atoms and molecules is, however, not an easy task, and the practical application of stoichiometry requires that we use the more readily measured property of mass.

Example 4.5 – Relating Masses of Reactants and Products

What mass of sodium hydroxide, NaOH, would be required to produce 16 g of the antacid milk of magnesia [magnesium hydroxide, Mg(OH)₂] by the following reaction?

MgCl₂(aq) + 2 NaOH(aq) → Mg(OH)₂(s) + 2 NaCl(aq)

Solution

The approach used previously in Example 4.3 and Example 4.4 is likewise used here; that is, we must derive an appropriate stoichiometric factor from the balanced chemical equation and use it to relate the amounts of the two substances of interest. In this case, however, masses (not molar amounts) are provided and requested, so additional steps of the sort learned in the previous chapter are required.

[latex]16 \cancel {g \: Mg(OH)_2} \; \frac {1 \cancel {mol \: Mg(OH)_2}}{58.3 \cancel {g \: Mg(OH)_2}} \; \frac {2 \cancel {mol \: NaOH}}{1 \cancel {mol \: Mg(OH)_2}} \; \frac {40.0 \: g \: NaOH}{\cancel {mol \: NaOH}} = 22 \: g \: NaOH[/latex]

The calculations required are outlined in this flowchart:

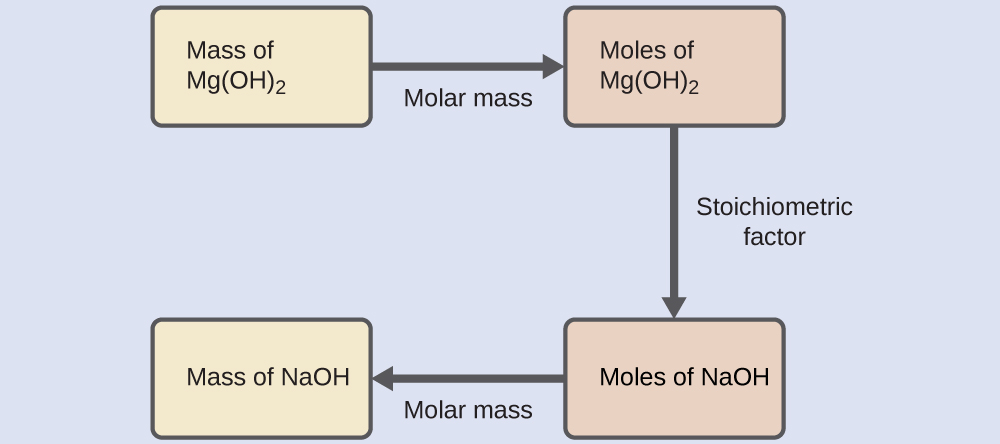
Check Your Learning

Example 4.6 – Relating Masses of Reactants

What mass of oxygen gas, O₂, from the air is consumed in the combustion of 702 g of octane, C₈H₁₈, one of the principal components of gasoline?

2 C₈H₁₈ + 25 O₂ → 16 CO₂ + 18 H₂O

Solution

The approach required here is the same as for the Example 4.5, differing only in that the provided and requested masses are both for reactant species.

[latex]702 \cancel {g \; C_8H_{18}} \; \frac {1 \cancel {mol \; C_8H_{18}}}{114.23 \cancel {g \; C_8H_{18}}} \; \frac {25 \cancel {mol \; O_2}}{2 \cancel {mol \; C_8H_{18}}} \; \frac {32.00 \: g \; O_2}{\cancel {mol \; O_2}} = 2.46 \times 10^3 \: g \; O_2[/latex]

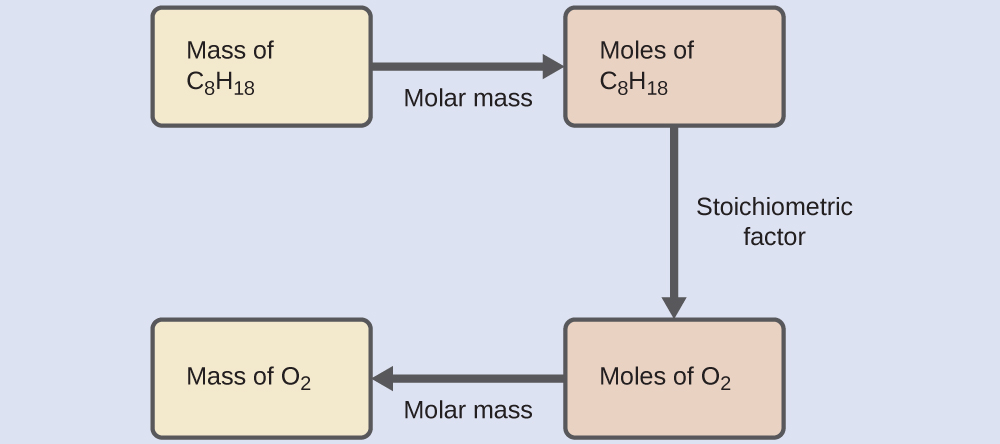
Check Your Learning

These examples illustrate just a few instances of reaction stoichiometry calculations. Numerous variations on the beginning and ending computational steps are possible depending upon what particular quantities are provided and sought (volumes, solution concentrations, and so forth). Regardless of the details, all these calculations share a common essential component: the use of stoichiometric factors derived from balanced chemical equations. Figure 4.5 provides a general outline of the various computational steps associated with many reaction stoichiometry calculations.

.

**Figure 4.5** The flowchart depicts the various computational steps involved in most reaction stoichiometry calculations.

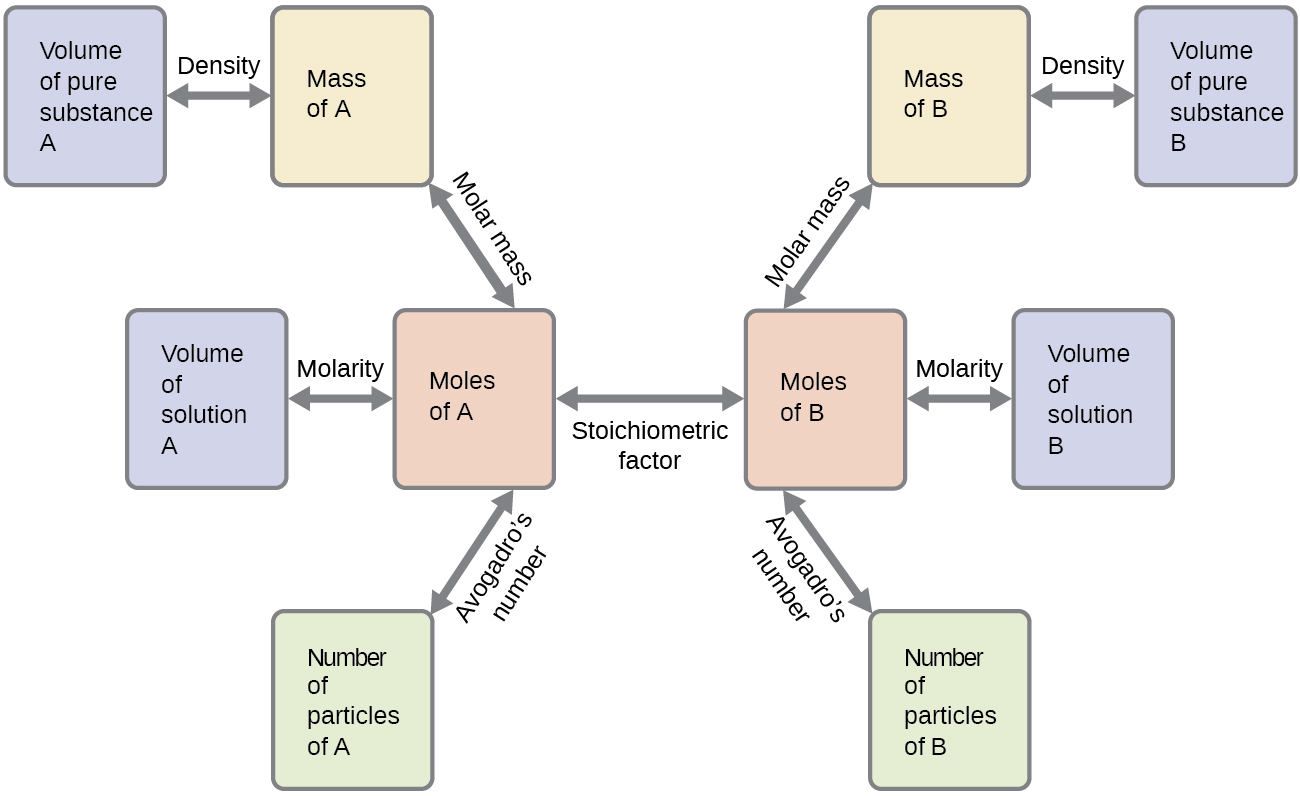
Chemistry in Everyday Life

Airbags

Airbags (Figure 4.6) are a safety feature provided in most automobiles since the 1990s. The effective operation of an airbag requires that it be rapidly inflated with an appropriate amount (volume) of gas when the vehicle is involved in a collision. This requirement is satisfied in many automotive airbag systems through the use of explosive chemical reactions, one common choice being the decomposition of sodium azide, NaN₃. When sensors in the vehicle detect a collision, an electrical current is passed through a carefully measured amount of NaN₃ to initiate its decomposition:

2 NaN₃(s) → 3 N₂(g) + 2 Na(s)

This reaction is very rapid, generating gaseous nitrogen that can deploy and fully inflate a typical airbag in a fraction of a second (~0.03–0.1 s). Among many engineering considerations, the amount of sodium azide used must be appropriate for generating enough nitrogen gas to fully inflate the air bag and ensure its proper function. For example, a small mass (~100 g) of NaN₃ will generate approximately 50 L of N₂.

.