5.2  Calorimetry

Nicole Bouvier-Brown; Saori Shiraki; J. Ryan Hunt; Emily Jarvis

Chapter 5 Thermochemistry

5.2 Calorimetry

Learning Objectives

By the end of this section, you will be able to:

Explain the technique of calorimetry
Calculate and interpret heat and related properties using typical calorimetry data

One technique we can use to measure the amount of heat involved in a chemical or physical process is known as calorimetry. Calorimetry is used to measure amounts of heat transferred to or from a substance. To do so, the heat is exchanged with a calibrated object (calorimeter). The temperature change measured by the calorimeter is used to derive the amount of heat transferred by the process under study. The measurement of heat transfer using this approach requires the definition of a system (the substance or substances undergoing the chemical or physical change) and its surroundings (all other matter, including components of the measurement apparatus, that serve to either provide heat to the system or absorb heat from the system).

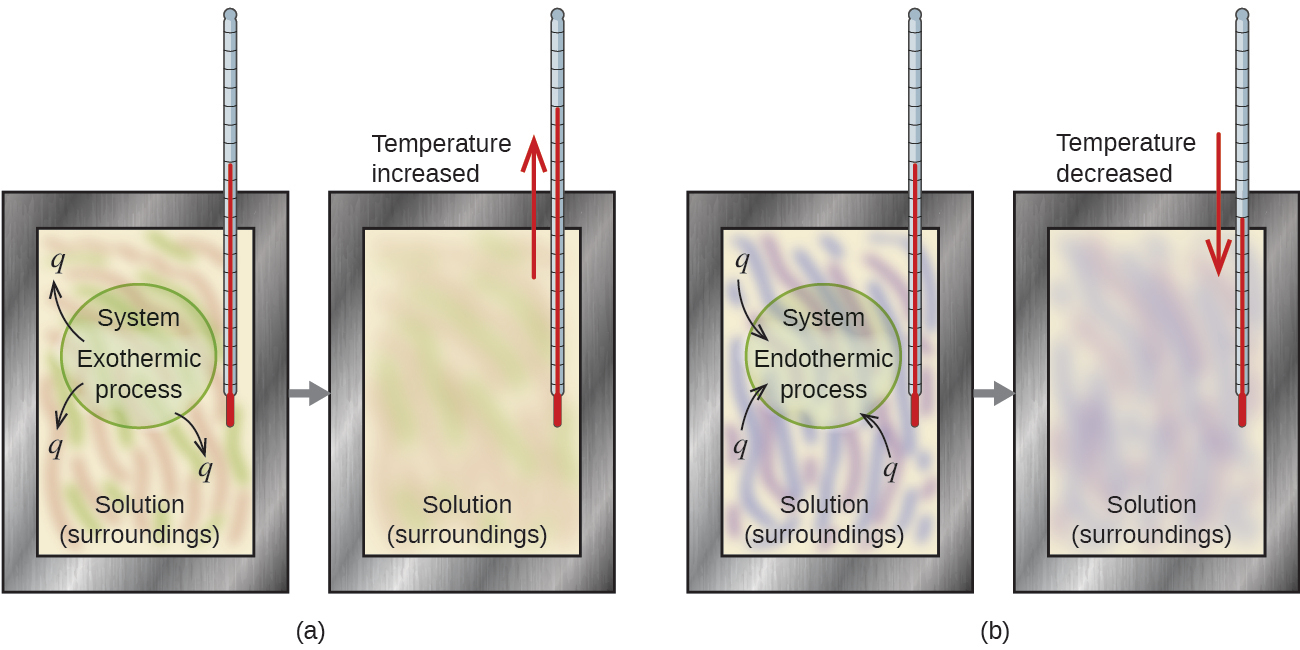
A calorimeter is a device used to measure the amount of heat involved in a chemical or physical process. For example, when an exothermic reaction occurs in solution in a calorimeter, the heat produced by the reaction is absorbed by the solution, which increases its temperature. When an endothermic reaction occurs, the heat required is absorbed from the thermal energy of the solution, which decreases its temperature (Figure 5.11). The temperature change, along with the specific heat and mass of the solution, can then be used to calculate the amount of heat involved in either case.

.

**Figure 5.11** In a calorimetric determination, either (a) an exothermic process occurs and heat, q, is negative, indicating that thermal energy is transferred from the system to its surroundings, or (b) an endothermic process occurs and heat, q, is positive, indicating that thermal energy is transferred from the surroundings to the system.

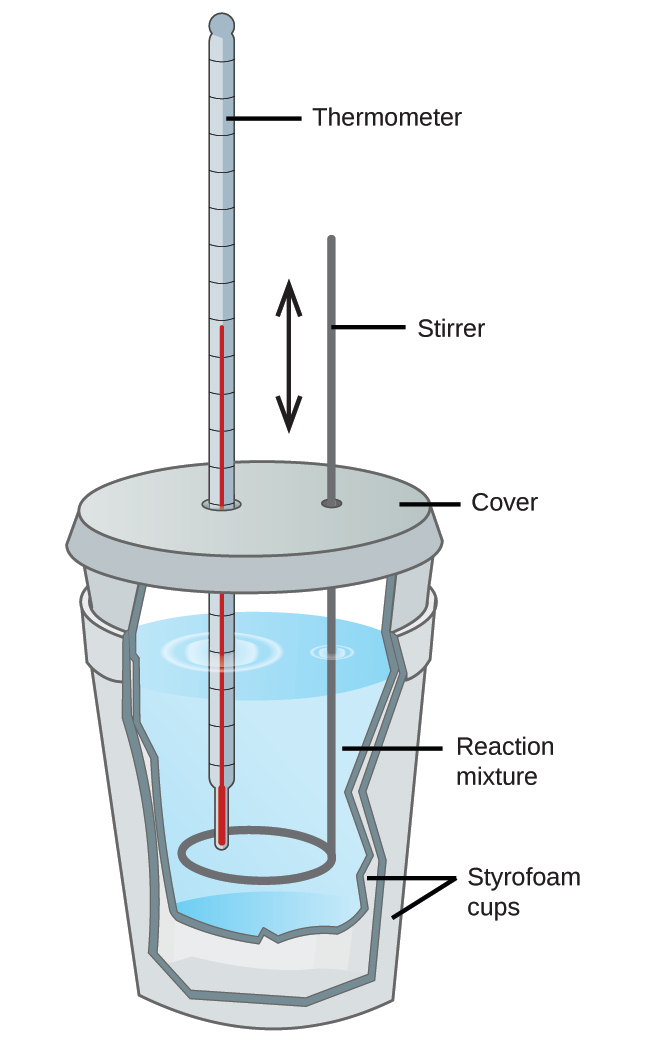
Calorimetry measurements are important in understanding the heat transferred in reactions involving everything from microscopic proteins to massive machines. Scientists use well-insulated calorimeters that all but prevent the transfer of heat between the calorimeter and its environment, which effectively limits the “surroundings” to the nonsystem components with the calorimeter (and the calorimeter itself). This enables the accurate determination of the heat involved in chemical processes, the energy content of foods, and so on. General chemistry students often use simple, relatively inexpensive calorimeters constructed from polystyrene cups (Figure 5.12). These easy-to-use “coffee cup” calorimeters allow more heat exchange with the outside environment, and therefore produce less accurate energy values.

.

**Figure 5.12** A simple calorimeter can be constructed from two polystyrene cups. A thermometer and stirrer extend through the cover into the reaction mixture.

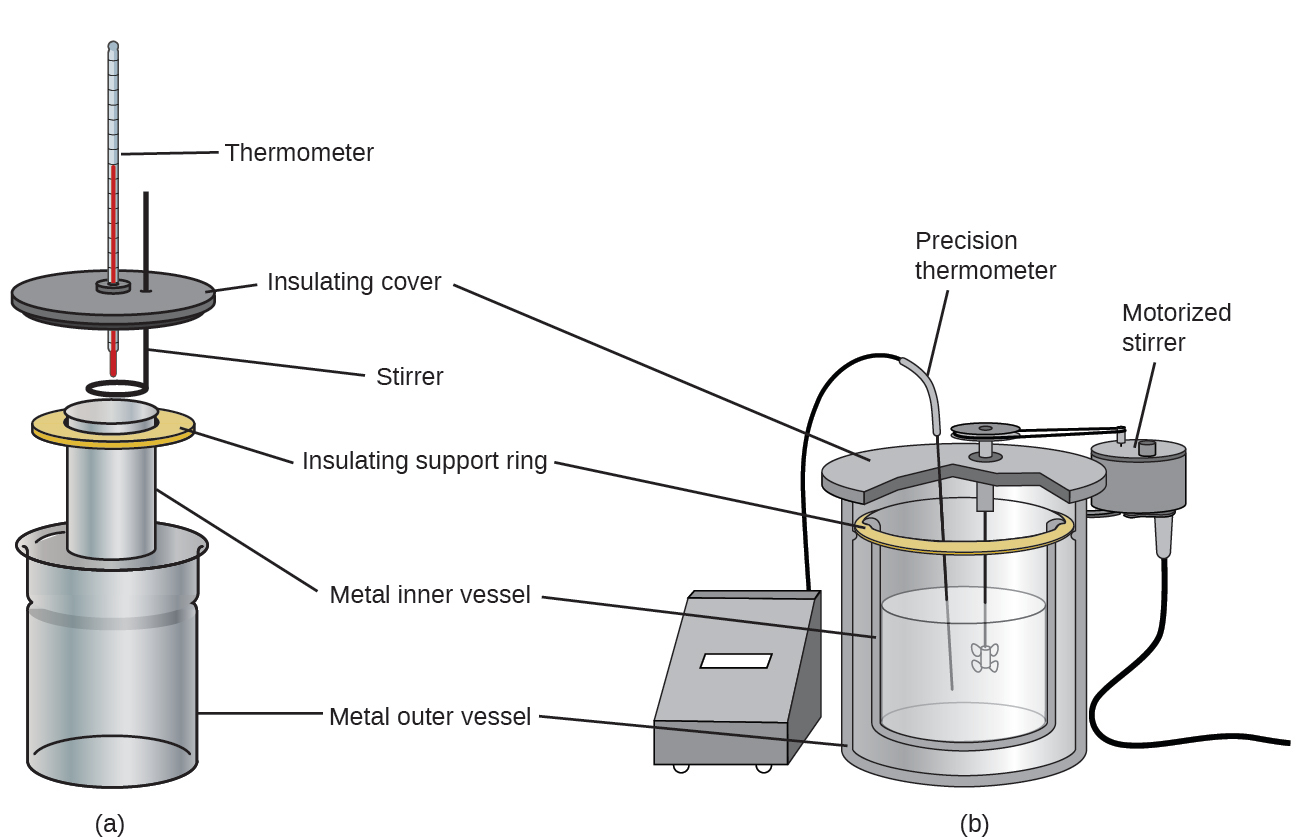
More expensive calorimeters used for industry and research typically have a well-insulated, fully enclosed reaction vessel, motorized stirring mechanism, and a more accurate temperature sensor (Figure 5.13).

.

**Figure 5.13** Commercial solution calorimeters range from (a) simple, inexpensive models for student use to (b) expensive, more accurate models for industry and research.

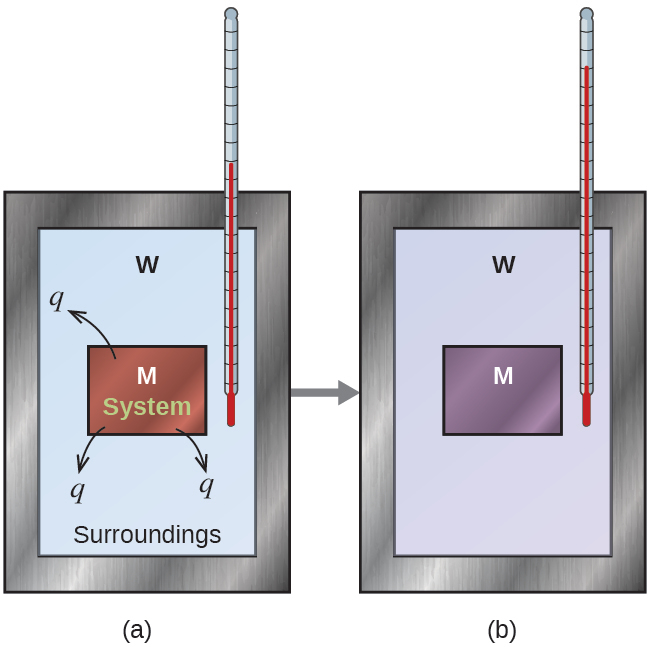
Before discussing the calorimetry of chemical reactions, consider a simpler example that illustrates the core idea behind calorimetry. Suppose we initially have a high-temperature substance, such as a hot piece of metal (M), and a low-temperature substance, such as cool water (W). If we place the metal in the water, heat will flow from M to W. The temperature of M will decrease, and the temperature of W will increase, until the two substances have the same temperature—that is, when they reach thermal equilibrium (Figure 5.14). If this occurs in a calorimeter, ideally all of this heat transfer occurs between the two substances, with no heat gained or lost by either to the external environment. Under these ideal circumstances, the net heat change is zero:

q_{s u b s t a n c e M} + q_{s u b s t a n c e W} = 0

This relationship can be rearranged to show that the heat gained by substance M is equal to the heat lost by substance W:

q_{s u b s t a n c e M} = - q_{s u b s t a n c e W}

The magnitude of the heat (change) is therefore the same for both substances, and the negative sign merely shows that q_{substance M} and q_{substance W} are opposite in direction of heat flow (gain or loss) but does not indicate the arithmetic sign of either q value (that is determined by whether the matter in question gains or loses heat, per definition). In the specific situation described, q_{substance M} is a negative value and q_{substance W} is positive, since heat is transferred from M to W.

.

**Figure 5.14** In a simple calorimetry process, (a) heat, q, is transferred from the hot metal, M, to the cool water, W, until (b) both are at the same temperature.

Example 5.3 – Heat Transfer between Substances at Different Temperatures

A 360.0-g piece of rebar (a steel rod used for reinforcing concrete) is dropped into 425 mL of water at 24.0°C. The final temperature of the water was measured as 42.7°C. Calculate the initial temperature of the piece of rebar. Assume the specific heat of steel is approximately the same as that for iron (Table 5.1), and that all heat transfer occurs between the rebar and the water (there is no heat exchange with the surroundings).

Solution

The temperature of the water increases from 24.0°C to 42.7°C, so the water absorbs heat. That heat came from the piece of rebar, which initially was at a higher temperature. Assuming that all heat transfer was between the rebar and the water, with no heat “lost” to the outside environment, then heat given off by rebar = −heat taken in by water, or:

q_{r e b a r} = - q_{w a t e r}

Since we know how heat is related to other measurable quantities, we have:

{(m c Δ T)}_{r e b a r} = - {(m c Δ T)}_{w a t e r}

Letting f = final and i = initial, in expanded form, this becomes:

m_{r e b a r} c_{r e b a r} (T_{f, r e b a r} - T_{i, r e b a r}) = - m_{w a t e r} c_{w a t e r} (T_{f, w a t e r} - T_{i, w a t e r})

The density of water is 1.0 g/mL, so 425 mL of water = 425 g. Noting that the final temperature of both the rebar and water is 42.7°C, substituting known values yields:

[latex][/latex]

[latex]\left( 360.0 \: g \right) \left( 0.449 \: J/g \cdot ^\circ C \right) \left( 42.7^\circ C - T_{i,rebar} \right)[/latex]

[latex]= -\left( 425 \: g \right) \left( 4.184 \: J/g \cdot ^\circ C \right) \left( 42.7^\circ C - 24.0^\circ C \right)[/latex]

[latex][/latex]

[latex]T_{i,rebar} = \frac { \left( 425 \: g \right) \left( 4.184 \: J/g \cdot ^\circ C \right) \left( 42.7^\circ C - 24.0^\circ C \right) }{ \left( 360.0 \: g \right) \left( 0.449 \: J/g \cdot ^\circ C \right)} + 42.7^\circ C[/latex]

[latex][/latex]

Solving this gives T_i,rebar = 248°C, so the initial temperature of the rebar was 248°C.

Check Your Learning

Click here to see how to solve this problem!

${(m c Δ T)}_{w a t e r} = - {(m c Δ T)}_{c o p p e r}$

$m_{w a t e r} c_{w a t e r} (T_{f, w a t e r} - T_{i, w a t e r}) = - m_{c o p p e r} c_{c o p p e r} (T_{f, c o p p e r} - T_{i, c o p p e r})$

Note that the final temperature of the water and the final temperature of the copper should be equal:

$T_{f} = T_{f, w a t e r} = T_{f, c o p p e r}$

We can therefore write

[latex]m_{water} \, c_{water} \left( T_f - T_{i,water} \right) = -m_{copper} \,c_{copper} \left( T_f - T_{i,copper} \right)[/latex]

Rearranging, we get…

[latex]m_{water} \, c_{water} \, T_f + m_{copper} \,c_{copper} \, T_f[/latex]

[latex]= m_{copper} \,c_{copper} \, T_{i,copper} + m_{water} \, c_{water} \, T_{i,water}[/latex]

Isolating T_f yields

[latex]T_f = \frac{m_{copper} \,c_{copper} \, T_{i,copper} + m_{water} \, c_{water} \, T_{i,water}}{m_{water} \, c_{water} +m_{copper} \,c_{copper}}[/latex]

Now we can solve for T_f:

[latex]T_f = \frac{(248 \, g) \, (0.385 \, J/g^oC)(314 \, ^\circ C) + (390 \, g) \, (4.184 \, J/g^\circ C)(22.6 \, ^\circ C)}{(390 \, g) \, (4.184 \, J/g^\circ C) +(248 \, g) \, (0.385 \, J/g^\circ C)}[/latex]

[latex]T_f = 38.7 \, ^\circ C[/latex]

This method can also be used to determine other quantities, such as the specific heat of an unknown metal.

Example 5.4 – Identifying a Metal by Measuring Specific Heat

A 59.7 g piece of metal that had been submerged in boiling water was quickly transferred into 60.0 mL of water initially at 22.0°C. The final temperature is 28.5°C. Use these data to determine the specific heat of the metal. Use this result to identify the metal.

Solution

Assuming perfect heat transfer, heat given off by metal = −heat taken in by water, or:

[latex]q_{metal} = -q_{water}[/latex]

In expanded form, this is:

[latex]m_{metal} \, c_{metal} \left( T_{f,metal} - T_{i,metal} \right) = -m_{water} \, c_{water} \left( T_{f,water} - T_{i,water} \right)[/latex]

[latex][/latex]

Noting that since the metal was submerged in boiling water, its initial temperature was 100.0°C; and that for water, 60.0 mL = 60.0 g; we have:

[latex][/latex]

[latex]\left( 59.7 \: g \right) c_{metal} \left( 28.5^\circ C - 100^\circ C \right)[/latex]

[latex]= - \left( 60.0 \: g \right) \left( 4.184 J/g \cdot ^\circ C \right) \left(28.5^\circ C - 22.0^\circ C \right)[/latex]

[latex][/latex]

Now we can solve for c_metal:

[latex][/latex]

[latex]c_{metal} = \frac { - \left( 60.0 \: g \right) \left( 4.184 \: J/g \cdot ^\circ C \right) \left( 6.5^\circ C \right)}{\left( 59.7 \: g \right) \left( -71.5^\circ C \right)} = 0.38 \: J/g \cdot ^\circ C[/latex]

[latex][/latex]

Comparing this with values in Table 5.1, our experimental specific heat is closest to the value for copper (0.39 J/g·°C), so we identify the metal as copper.

[latex][/latex]

Check Your Learning

Compare the calculated specific heat you just calculated to those in Table 5.1. You should find that the specific heat is close to that of two different metals.

What is the identity of the unknown metal? How do you know?

The metal is lead.

The calculated specific heat is close to that of lead and gold. The problem indicates that the unkown metal is silver/gray, so it cannot be gold. The unknown metal must therefore be lead.

When we use calorimetry to determine the heat involved in a chemical reaction, the same principles we have been discussing apply. The amount of heat absorbed by the calorimeter is often small enough that we can neglect it (though not for highly accurate measurements, as discussed later), and the calorimeter minimizes energy exchange with the outside environment. Because energy is neither created nor destroyed during a chemical reaction, the heat produced or consumed in the reaction (the “system”), q_reaction, plus the heat absorbed or lost by the solution (the “surroundings”), q_solution, must add up to zero:

q_{r e a c t i o n} + q_{s o l u t i o n} = 0

This means that the amount of heat produced or consumed in the reaction equals the amount of heat absorbed or lost by the solution:

q_{r e a c t i o n} = - q_{s o l u t i o n}

This concept lies at the heart of all calorimetry problems and calculations.

Example 5.5 – Heat Produced by an Exothermic Reaction

When 50.0 mL of 1.00 M HCl(aq) and 50.0 mL of 1.00 M NaOH(aq), both at 22.0°C, are added to a coffee cup calorimeter, the temperature of the mixture reaches a maximum of 28.9°C. What is the approximate amount of heat produced by this reaction?

HCl(aq) + NaOH(aq) → NaCl(aq) + H₂O(l)

Solution

To visualize what is going on, imagine that you could combine the two solutions so quickly that no reaction took place while they mixed; then after mixing, the reaction took place. At the instant of mixing, you have 100.0 mL of a mixture of HCl and NaOH at 22.0°C. The HCl and NaOH then react until the solution temperature reaches 28.9°C.

The heat given off by the reaction is equal to that taken in by the solution. Therefore:

q_{r e a c t i o n} = - q_{s o l u t i o n}

(It is important to remember that this relationship only holds if the calorimeter does not absorb any heat from the reaction, and there is no heat exchange between the calorimeter and the outside environment.)

Next, we know that the heat absorbed by the solution depends on its specific heat, mass, and temperature change:

q_{s o l u t i o n} = {(m c Δ T)}_{s o l u t i o n}

To proceed with this calculation, we need to make a few more reasonable assumptions or approximations. Since the solution is aqueous, we can proceed as if it were water in terms of its specific heat and mass values. The density of water is approximately 1.0 g/mL, so 100.0 mL has a mass of about 1.0 × 10² g (two significant figures). The specific heat of water is approximately 4.184 J/g·°C, so we use that for the specific heat of the solution. Substituting these values gives:

[latex]q_{solution} = \left(1.0 \times 10^2 \: g \right) \left( 4.184 \: J/g \cdot ^\circ C \right) \left( 28.9^\circ C - 22.0^\circ C \right) = 2.9 \times 10^3 \: J[/latex]

[latex][/latex]

Finally, since we are trying to find the heat of the reaction, we have:

q_{r e a c t i o n} = - q_{s o l u t i o n} = - 2.9 \times 10^{3} J

The negative sign indicates that the reaction is exothermic. It produces 2.9 kJ of heat.

Check Your Learning

What assumptions did you make to answer the above question?

no heat is absorbed by the calorimeter/container
no heat is lost to the surroundings
the specific heat and mass of the solution are the same as those for water

Portrait of a Chemist

Reatha Clark King

Reatha Clark King (Figure 5.15) is an American chemist, professor, and corporate executive. After receiving her PhD in thermochemistry from the University of Chicago in 1963, she became the first black woman to work at the National Bureau of Standards in Washington, D.C.

.

**Figure 5.15** Reatha Clark King in 2009 (photo courtesy of “VocalEssence Ensemble Singers”/Flickr).

During her time at the National Bureau of Standards (1963 – 1968), King performed careful calorimetric experiments to determine the enthalpies of formation for various fluorine compounds. Her work was important to NASA in their quest for better rocket fuels. Techniques that King developed for precise flame fluorine calorimetry are still in use today. Later, King served as professor of chemistry and associate dean for academic affairs at York College in New York, president of Metropolitan State University in Minnesota, vice president of the General Mills Corporation, and president and executive director of the General Mills Foundation.

Watch the video below to learn more about Dr. King.

Chemistry in Everyday Life

Thermochemistry of Hand Warmers

When working or playing outdoors on a cold day, you might use a hand warmer to warm your hands (Figure 5.16). A common reusable hand warmer contains a supersaturated solution of NaC₂H₃O₂ (sodium acetate) and a metal disc. Bending the disk creates nucleation sites around which the metastable NaC₂H₃O₂ quickly crystallizes (a later chapter on solutions will investigate saturation and supersaturation in more detail).

The process

NaC₂H₃O₂(aq) → NaC₂H₃O₂(s)

[latex][/latex]

is exothermic, and the heat produced by this process is absorbed by your hands, thereby warming them (at least for a while). If the hand warmer is reheated, the NaC₂H₃O₂ redissolves and can be reused.

.

**Figure 5.16** Chemical hand warmers produce heat that warms your hand on a cold day. In this one, you can see the metal disc that initiates the exothermic precipitation reaction. (credit: modification of work by Science Buddies TV/YouTube)

Another common hand warmer produces heat when it is ripped open, exposing iron and water in the hand warmer to oxygen in the air. One simplified version of this exothermic reaction is

2 Fe(s) + 3/2 O₂(g) → Fe₂O₃(s).

[latex][/latex]

Salt in the hand warmer catalyzes the reaction, so it produces heat more rapidly; cellulose, vermiculite, and activated carbon help distribute the heat evenly. Other types of hand warmers use lighter fluid (a platinum catalyst helps lighter fluid oxidize exothermically), charcoal (charcoal oxidizes in a special case), or electrical units that produce heat by passing an electrical current from a battery through resistive wires.

Link to Learning

This link shows the precipitation reaction that occurs when the disk in a chemical hand warmer is flexed.

Example 5.6 – Heat Flow in an Instant Ice Pack

When solid ammonium nitrate dissolves in water, the solution becomes cold. This is the basis for an “instant ice pack” (Figure 5.17). When 3.21 g of solid NH₄NO₃ dissolves in 50.0 g of water at 24.9°C in a calorimeter, the temperature decreases to 20.3°C.

Calculate the value of q for this reaction and explain the meaning of its arithmetic sign. State any assumptions that you made.

.

**Figure 5.17** An instant cold pack consists of a bag containing solid ammonium nitrate and a second bag of water. When the bag of water is broken, the pack becomes cold because the dissolution of ammonium nitrate is an endothermic process that removes thermal energy from the water. The cold pack then removes thermal energy from your body.

Solution

We assume that the calorimeter prevents heat transfer between the solution and its external environment (including the calorimeter itself), in which case:

q_{r x n} = - q_{s o l n}

with “rxn” and “soln” used as shorthand for “reaction” and “solution,” respectively.

Assuming also that the specific heat of the solution is the same as that for water, we have:

[latex]q_{rxn} = -q_{soln} = - \left( cm \Delta T \right) _{soln}[/latex]

[latex]= - \left[ \left( 53.2 \: g \right) \left(4.184 \: J/g \cdot ^\circ C \right) \left( 20.3^\circ C - 24.9^\circ C \right) \right][/latex]

[latex]= - \left[ \left( 53.2 \: g \right) \left( 4.184 \: J/g \cdot ^\circ C \right) \left( -4.6^oC \right) \right][/latex]

[latex]= + 1.0 \times 10^3 \: J = +1.0 \: kJ[/latex]

[latex][/latex]

The positive sign for q indicates that the dissolution is an endothermic process.

Check Your Learning

If the amount of heat absorbed by a calorimeter is too large to neglect or if we require more accurate results, then we must take into account the heat absorbed both by the solution and by the calorimeter.

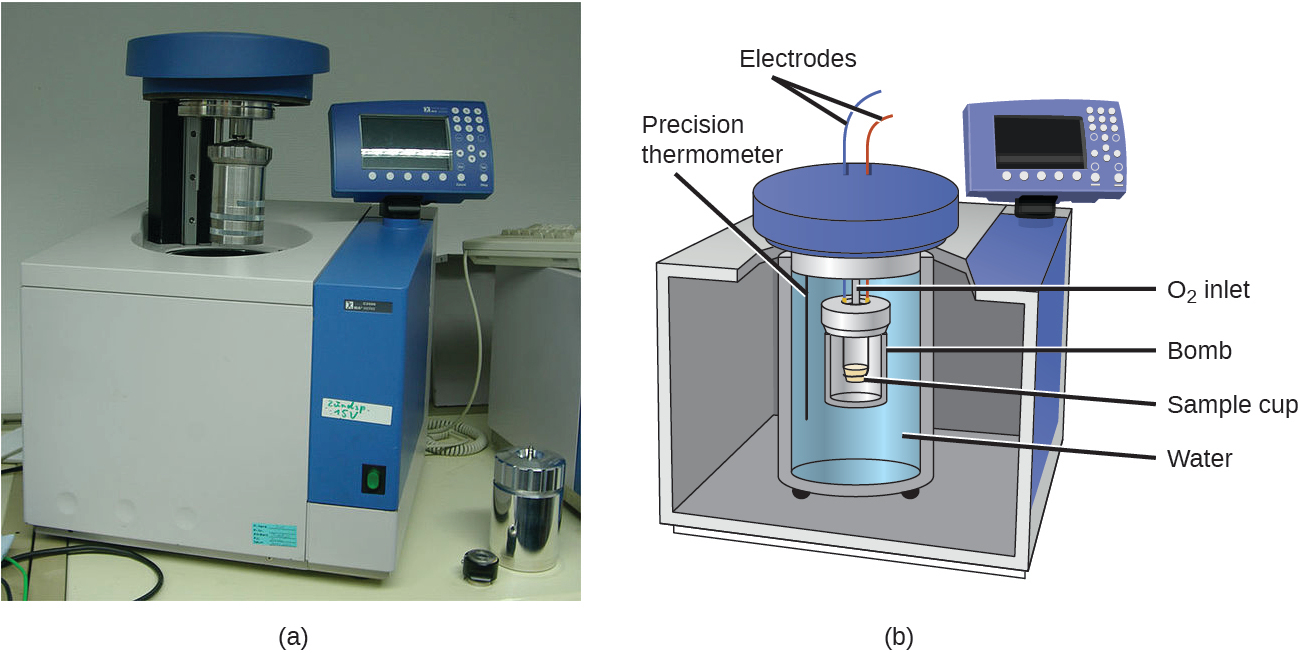
The calorimeters described are designed to operate at constant (atmospheric) pressure and are convenient to measure heat flow accompanying processes that occur in solution. A different type of calorimeter that operates at constant volume, colloquially known as a bomb calorimeter, is used to measure the energy produced by reactions that yield large amounts of heat and gaseous products, such as combustion reactions. (The term “bomb” comes from the observation that these reactions can be vigorous enough to resemble explosions that would damage other calorimeters.) This type of calorimeter consists of a robust steel container (the “bomb”) that contains the reactants and is itself submerged in water (Figure 5.18).

The sample is placed in the bomb, which is then filled with oxygen at high pressure. A small electrical spark is used to ignite the sample. The energy produced by the reaction is absorbed by the steel bomb and the surrounding water. The temperature increase is measured and, along with the known heat capacity of the calorimeter, is used to calculate the energy produced by the reaction. Bomb calorimeters require calibration to determine the heat capacity of the calorimeter and ensure accurate results. The calibration is accomplished using a reaction with a known q, such as a measured quantity of benzoic acid ignited by a spark from a nickel fuse wire that is weighed before and after the reaction. The temperature change produced by the known reaction is used to determine the heat capacity of the calorimeter. The calibration is generally performed each time before the calorimeter is used to gather research data.

.

**Figure 5.18** (a) A bomb calorimeter is used to measure heat produced by reactions involving gaseous reactants or products, such as combustion. (b) The reactants are contained in the gas-tight “bomb,” which is submerged in water and surrounded by insulating materials. (credit a: modification of work by “Harbor1”/Wikimedia commons)

Link to Learning

Click on this link to view how a bomb calorimeter is prepared for action.

This site shows calorimetric calculations using sample data.

Example 5.7 – Bomb Calorimetry

When 3.12 g of glucose, C₆H₁₂O₆, is burned in a bomb calorimeter, the temperature of the calorimeter increases from 23.8°C to 35.6°C. The calorimeter contains 775 g of water, and the bomb itself has a heat capacity of 893 J/°C. How much heat was produced by the combustion of the glucose sample?

Solution

The combustion produces heat that is primarily absorbed by the water and the bomb. (The amounts of heat absorbed by the reaction products and the unreacted excess oxygen are relatively small and dealing with them is beyond the scope of this text. We will neglect them in our calculations.)

The heat produced by the reaction is absorbed by the water and the bomb:

[latex]q_{rxn} = - \left( q_{water} + q_{bomb} \right)[/latex]

[latex]= - \left[ \left( mc \Delta T \right)_{water} + \left( C \Delta T \right)_{bomb} \right][/latex]

[latex]= - ( 775 \: g ) ( 4.184 \: J/g \cdot ^\circ C)( 35.6^\circ C - 23.8^\circ C)[/latex]

[latex]- \left( 893 \: J/^oC \right) \left( 35.6^\circ C - 23.8^\circ C \right)[/latex]

[latex]= - 38,300 \: J - 10,500 \: J[/latex]

[latex]= - 48,800 \: J = -48.8 \: kJ[/latex]

[latex][/latex]

This reaction released 48.8 kJ of heat when 3.12 g of glucose was burned.

Check Your Learning

Since the first one was constructed in 1899, 35 calorimeters have been built to measure the heat produced by a living person.^[1] These whole-body calorimeters of various designs are large enough to hold an individual human being. More recently, whole-room calorimeters allow for relatively normal activities to be performed, and these calorimeters generate data that more closely reflect the real world. These calorimeters are used to measure the metabolism of individuals under different environmental conditions, different dietary regimes, and with different health conditions, such as diabetes.

Carla Prado’s team at University of Alberta undertook whole-body calorimetry to understand the energy expenditures of women who had recently given birth. Studies like this help develop better recommendations and regimens for nutrition, exercise, and general wellbeing during this period of significant physiological change.

Chemistry in Everyday Life

Measuring Nutritional Calories

In your day-to-day life, you may be more familiar with energy being given in Calories, or nutritional calories, which are used to quantify the amount of energy in foods. One calorie (cal) = exactly 4.184 joules, and one Calorie (note the capitalization) = 1000 cal, or 1 kcal. (This is approximately the amount of energy needed to heat 1 kg of water by 1°C.)

The macronutrients in food are proteins, carbohydrates, and fats. Nutritional labels on food packages show the caloric content of one serving of the food, as well as the breakdown into Calories from each of the three macronutrients (Figure 5.19).

.

**Figure 5.19** (a) Macaroni and cheese contain energy in the form of the macronutrients in the food. (b) The food’s nutritional information is shown on the package label. In the US, the energy content is given in Calories (per serving); the rest of the world usually uses kilojoules. (credit a: modification of work by “Rex Roof”/Flickr)

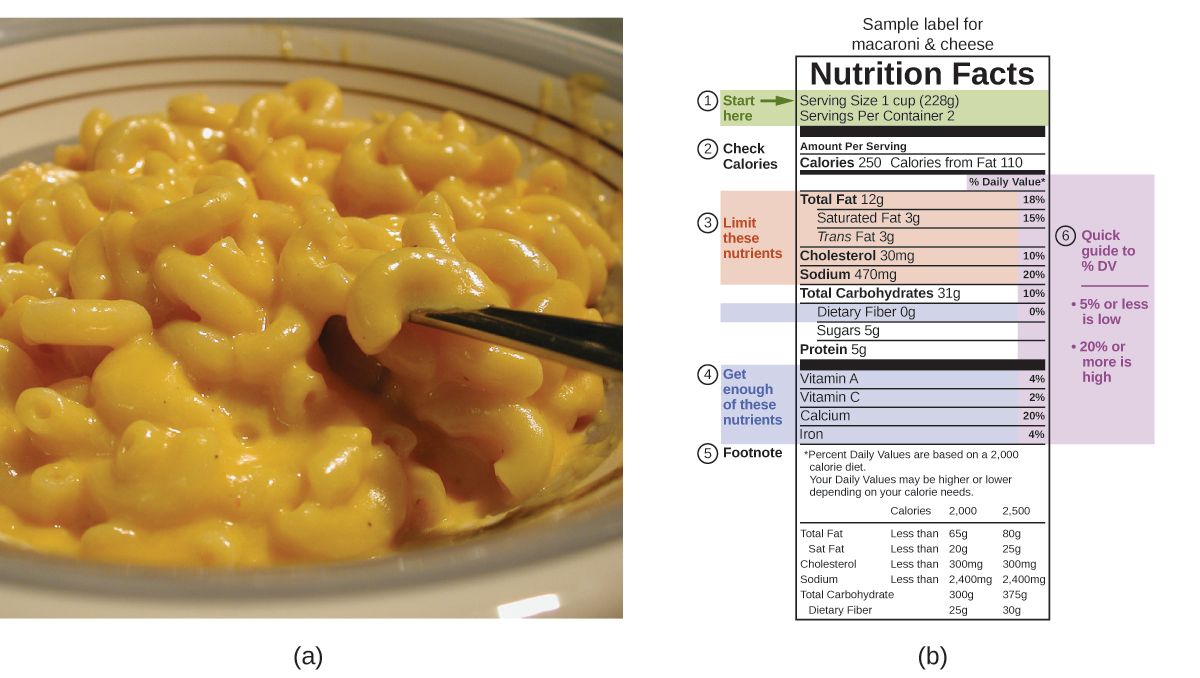
You can use food labels to count your Calories. But where do the values come from? And how accurate are they? The caloric content of foods can be determined using bomb calorimetry; that is, by burning the food and measuring the energy it contains. A sample of food is weighed, mixed in a blender, freeze-dried, ground into powder, and formed into a pellet. The pellet is burned inside a bomb calorimeter, and the measured temperature change is converted into energy per gram of food.

Today, the caloric content on food labels is derived using a method called the Atwater system that uses the average caloric content of the food’s macronutrients. Proteins and carbohydrates provide about 4 Calories per gram, and fats and oils provide about 9 Calories/g. To determine the energy content of a food, the quantities of carbohydrate, protein, and fat are each multiplied by the average Calories per gram for each and the products summed to obtain the total energy. For the example shown in (b), the total energy per 228-g portion is calculated by:

[latex]\left( 5 \: g \: protein \times 4 \: Calories/g \right) + \left( 31 \: g \: carb \times 4 \: Calories/g\right)[/latex]

[latex]+ \left( 12 \: g \: fat \times 9 \: Calories/g \right) = 252 \: Calories[/latex]

[latex][/latex]

The fiber content, which consists of indigestible carbohydrates, is typically subtracted from this total.

Link to Learning

Click on this link to access the US Department of Agriculture (USDA) National Nutrient Database, containing nutritional information on over 8000 foods.

Media Attributions

Reatha_King_2009

Francis D. Reardon et al. “The Snellen human calorimeter revisited, re-engineered and upgraded: Design and performance characteristics.” Medical and Biological Engineering and Computing 8 (2006)721–28, http://link.springer.com/article/10.1007/s11517-006-0086-5. ↵

5.2 Calorimetry

Learning Objectives

Portrait of a Chemist

Reatha Clark King

Chemistry in Everyday Life

Thermochemistry of Hand Warmers

Link to Learning

Link to Learning

Chemistry in Everyday Life

Measuring Nutritional Calories

Link to Learning

Media Attributions

License

Share This Book