Chapter 5 Thermochemistry
5.4Β Determining Reaction Enthalpies
Learning Objectives
By the end of this section, you will be able to:
- Calculate enthalpy changes for various chemical reactions
- Explain Hessβs law and use it to compute reaction enthalpies
Standard Enthalpy of Formation
A standard enthalpy of formation ΞHfβΒ°βΒ is an enthalpy change for a reaction in which exactly 1 mole of a pure substance is formed from free elements in their most stable states under standard state conditions. These values are especially useful for computing or predicting enthalpy changes for chemical reactions that are impractical or dangerous to carry out, or for processes for which it is difficult to make measurements. If we have values for the appropriate standard enthalpies of formation, we can determine the enthalpy change for any reaction, which we will practice in the next section on Hessβs law.
The standard enthalpy of formation of CO2(g) is β393.5 kJ/mol. This is the enthalpy change for the exothermic reaction:
starting with the reactants at a pressure of 1 atm and 25Β°C (with the carbon present as graphite, the most stable form of carbon under these conditions) and ending with one mole of CO2, also at 1 atm and 25Β°C. For nitrogen dioxide, NO2(g), ΞHfβ° is 33.2 kJ/mol. This is the enthalpy change for the reaction:
A reaction equation with 1/2 mole of N2 and 1 mole of O2 is correct in this case because the standard enthalpy of formation always refers to 1 mole of product, NO2(g).
You will find a table of standard enthalpies of formation of many common substances in Appendix G. These values indicate that formation reactions range from highly exothermic (such as β2984 kJ/mol for the formation of P4O10) to strongly endothermic (such as +226.7 kJ/mol for the formation of acetylene, C2H2). By definition, the standard enthalpy of formation of an element in its most stable form is equal to zero under standard conditions, which is 1 atm for gases and 1 M for solutions.
Example 5.11 – Evaluating an Enthalpy of Formation
Ozone, O3(g), forms from oxygen, O2(g), by an endothermic process. Ultraviolet radiation is the source of the energy that drives this reaction in the upper atmosphere. Assuming that both the reactants and products of the reaction are in their standard states, determine the standard enthalpy of formation ΞHfΒ° of ozone from the following information:
Solution
ΞHfΒ° is the enthalpy change for the formation of one mole of a substance in its standard state from the elements in their standard states. Thus, ΞHf° for O3(g) is the enthalpy change for the reaction:
[latex][/latex]
For the formation of 2 mol of O3(g), ΞHΒ° = +286 kJ.
This ratio, 286β kJ/(2β molβ O3), can be used as a conversion factor to find the heat produced when 1 mole of O3(g) is formed, which is the enthalpy of formation for O3(g):
Therefore, ΞHfβΒ°(O3(g)) = +143kJ/mol.
Check Your Learning
Example 5.12 – Writing Reaction Equations for ΞHfβΒ°
Write the heat of formation reaction equations for:
(a)Β C2H5OH(l)
(b)Β Ca3(PO4)2(s)
Solution
Remembering that ΞHfβΒ° reaction equations are for forming 1 mole of the compound from its constituent elements under standard conditions, we have:
(a)Β 2 C(s, graphite) + 3 H2(g) +β12 O2(g)β ββ C2H5OH(l)
(b)Β 3 Ca(s) +β12 P4(s) + 4 O2(g)β ββ Ca3(PO4)2(s)
Note: The standard state of carbon is graphite, and phosphorus exists as P4.
Check Your Learning
Write the heat of formation reaction equations for:
C2H5OC2H5(l)
4 C(s,β graphite) + 5 H2(g) +β1/2 O2(g)β ββ C2H5OC2H5(l)
Na2CO3(s)
2 Na(s) + C(s,β graphite) +β3/2 O2(g)β ββ Na2CO3(s)
Hessβs Law
There are two ways to determine the amount of heat involved in a chemical change: measure it experimentally, or calculate it from other experimentally determined enthalpy changes. Some reactions are difficult, if not impossible, to investigate and make accurate measurements for experimentally. And even when a reaction is not hard to perform or measure, it is convenient to be able to determine the heat involved in a reaction without having to perform an experiment.
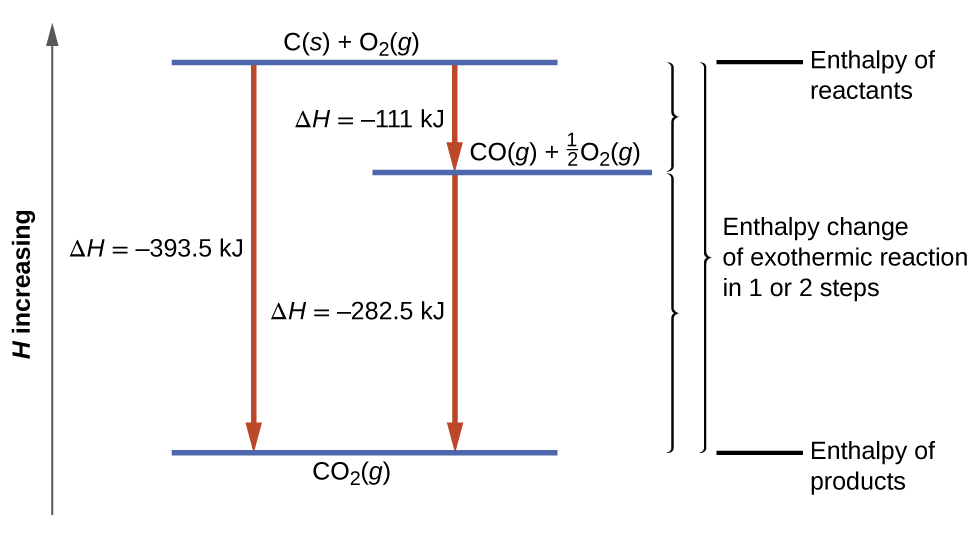
This type of calculation usually involves the use of Hessβs law, which states: If a process can be written as the sum of several stepwise processes, the enthalpy change of the total process equals the sum of the enthalpy changes of the various steps. Hessβs law is valid because enthalpy is a state function: enthalpy changes depend only on where a chemical process starts and ends, but not on the path it takes from start to finish. For example, we can think of the reaction of carbon with oxygen to form carbon dioxide as occurring either directly or by a two-step process. The direct process is written:
In the two-step process, first carbon monoxide is formed:
Then, carbon monoxide reacts further to form carbon dioxide:
The equation describing the overall reaction is the sum of these two chemical changes:
ββStep 1: β C(s) + 1/2 O2(g)β ββ CO(g)
Because the CO produced in Step 1 is consumed in Step 2, the net change is:
According to Hessβs law, the enthalpy change of the reaction will equal the sum of the enthalpy changes of the steps.
ββStep 1: β C(s) + 1/2 O2(g)β ββ CO(g)βββ ΞHΒ° = β111β kJ
The result is shown in Figure 5.25. We see that ΞH of the overall reaction is the same whether it occurs in one step or two. This finding (overall ΞH for the reaction = sum of ΞH values for reaction βstepsβ in the overall reaction) is true in general for chemical and physical processes.
Before we further practice using Hessβs law, let us recall two important features of ΞH:
- ΞH is directly proportional to the quantities of reactants or products.
For example, the enthalpy change for the reaction forming 1 mole of NO2(g) is +33.2 kJ:
When 2 moles of NO2 (twice as much) are formed, the ΞH will be twice as large:
In general, if we multiply or divide an equation by a number, then the enthalpy change should also be multiplied or divided by the same number.
2. ΞH for a reaction in one direction is equal in magnitude and opposite in sign to ΞH for the reaction in the reverse direction.
For example, given that:
Then, for the βreverseβ reaction, the enthalpy change is also βreversedβ:
Example 5.13 – Stepwise Calculation of ΞHfβΒ° Using Hessβs Law
Determine the enthalpy of formation, ΞHfβΒ°, of FeCl3(s) from the enthalpy changes of the following two-step process that occurs under standard state conditions:
Solution
We are trying to find the standard enthalpy of formation of FeCl3(s), which is equal to ΞHΒ° for the reaction:
Looking at the reactions, we see that the reaction for which we want to find ΞHΒ° is the sum of the two reactions with known ΞH values, so we must sum their ΞH’s:
ββFe(s) + Cl2(g)β ββ FeCl2(s)ββββΒ ΞHΒ° = β341.8β kJ
The enthalpy of formation, ΞHfβΒ°, of FeCl3(s) is β399.5 kJ/mol.
Check Your Learning
Here is a less straightforward example that illustrates the thought process involved in solving many Hessβs law problems. It shows how we can find many standard enthalpies of formation (and other values of ΞH) if they are difficult to determine experimentally.
Example 5.14 – A More Challenging Problem Using Hessβs Law
Chlorine monofluoride can react with fluorine to form chlorine trifluoride:
(i)Β ClF(g) + F2(g)β ββ ClF3(g)ββΞHΒ° = ?
Use the reactions here to determine the ΞHΒ° for reaction (i):
(ii)Β 2 OF2(g)β ββ O2(g) + 2 F2(g)ββββββββΒ Β ΞH(ii)βΒ° = β49.4β kJ
Solution
Our goal is to manipulate and combine reactions (ii), (iii), and (iv) such that they add up to reaction (i). Going from left to right in (i), we first see that ClF(g) is needed as a reactant. This can be obtained by multiplying reaction (iii) by 1/2, which means that the ΞHΒ° change is also multiplied by 1/2:
ClF(g) + 1/2 O2(g)β ββ 1/2 Cl2O(g) +β1/2 OF2(g)
Next, we see that F2 is also needed as a reactant. To get this, reverse and halve reaction (ii), which means that the ΞHΒ° changes sign and is halved:
To get ClF3 as a product, reverse (iv), changing the sign of ΞHΒ°:
Now check to make sure that these reactions add up to the reaction we want:
ββClF(g) + 1/2 O2(g)β ββ 1/2 Cl2O(g) +β1/2 OF2(g)βΒ Β ΞHΒ° = +107.0 kJ
- Reactants 1/2 O2 and 1/2 O2 cancel out product O2
- Product 1/2 Cl2O cancels reactant 1/2 Cl2O
- Reactant 3/2 OF2 is cancelled by products 1/2 OF2 and OF2
This leaves only reactants ClF(g) and F2(g) and product ClF3(g), which are what we want. Since summing these three modified reactions yields the reaction of interest, summing the three modified ΞHΒ° values will give the desired ΞHΒ°:
Check Your Learning
We also can use Hessβs law to determine the enthalpy change of any reaction if the corresponding enthalpies of formation of the reactants and products are available. The stepwise reactions we consider are: (i) decompositions of the reactants into their component elements (for which the enthalpy changes are proportional to the negative of the enthalpies of formation of the reactants), followed by (ii) re-combinations of the elements to give the products (with the enthalpy changes proportional to the enthalpies of formation of the products). The standard enthalpy change of the overall reaction is therefore equal to: (ii) the sum of the standard enthalpies of formation of all the products plus (i) the sum of the negatives of the standard enthalpies of formation of the reactants. This is usually rearranged slightly to be written as follows, with β representing βthe sum ofβ and n standing for the stoichiometric coefficients:
The following example shows in detail why this equation is valid, and how to use it to calculate the enthalpy change for a reaction of interest.
Example 5.15 – Using Hessβs Law
What is the standard enthalpy change for the reaction:
Solution (Using the Equation):
Use the special form of Hessβs law given previously, and values from (Appendix G):
β [latex]\Delta H^{\circ} = \Sigma n \Delta H^{\circ}_f (products) - \Sigma n \Delta H^{\circ}_f (reactants)[/latex]
Solution (Supporting Why the General Equation Is Valid):
Alternatively, we can write this reaction as the sum of the decompositions of 3NO2(g) and H2O(l) into their constituent elements, and the formation of 2HNO3(aq) and NO(g) from their constituent elements. Writing out these reactions, and noting their relationships to the ΞHfββ values for these compounds (from Appendix G ), we have:
ββ3 NO2(g)β ββ 3/2 N2(g) + 3 O2(g)βΒ Β Β Β βΒ Β ΞH1βΒ° = [-3ΓΞHfΒ°β(NO2)] = β99.6kJ
Summing these reaction equations gives the reaction we are interested in:
Summing their enthalpy changes gives the value we want to determine:
So the standard enthalpy change for this reaction is ΞHΒ° = β138.4 kJ.
Note that this result was obtained by (1) multiplying the ΞHfβΒ° of each product by its stoichiometric coefficient and summing those values, (2) multiplying the ΞHfβΒ° of each reactant by its stoichiometric coefficient and summing those values, and then (3) subtracting the result found in (2) from the result found in (1). This is also the procedure in using the general equation, as shown.
Check Your Learning
