Chapter 9 Gases
9.5 Stoichiometry of Gaseous Substances, Mixtures and Reactions
Learning Objectives
By the end of this section, you will be able to:
- State Dalton’s law of partial pressures and use it in calculations involving gaseous mixtures
- Perform stoichiometric calculations involving gaseous substance
The Pressure of a Mixture of Gases: Dalton’s Law
Unless they chemically react with each other, the individual gases in a mixture of gases do not affect each other’s pressure. Each individual gas in a mixture exerts the same pressure that it would exert if it were present alone in the container (Figure 9.21). The pressure exerted by each individual gas in a mixture is called its partial pressure. This observation is summarized by Dalton’s law of partial pressures: The total pressure of a mixture of ideal gases is equal to the sum of the partial pressures of the component gases:
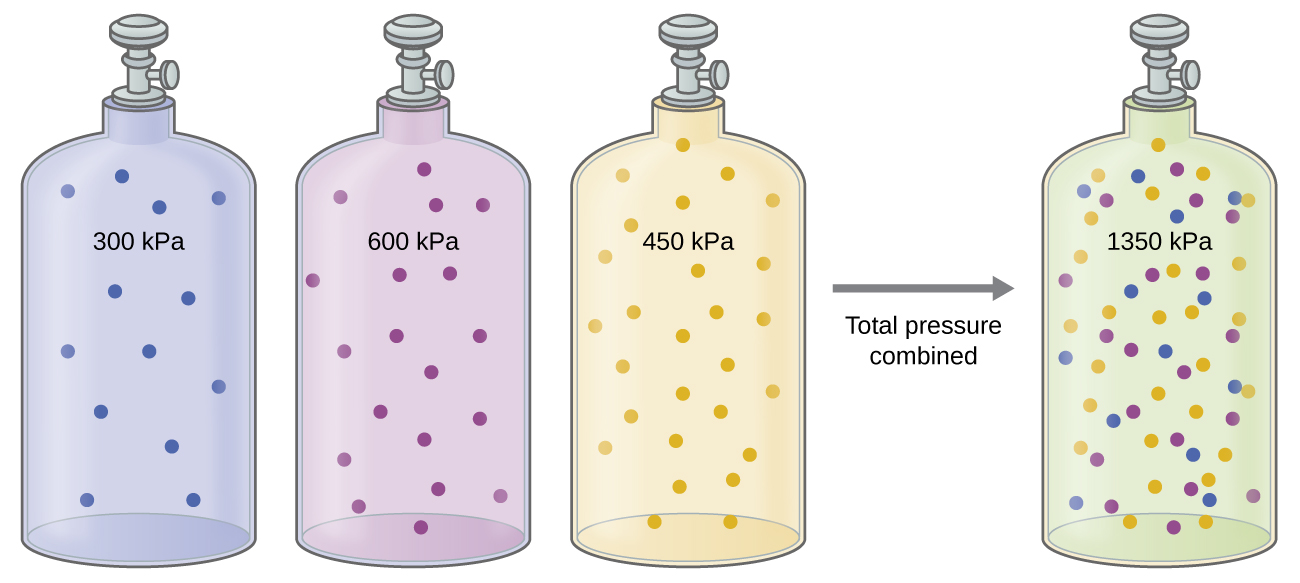
The partial pressure of gas A is related to the total pressure of the gas mixture via its mole fraction (X), a unit of concentration defined as the number of moles of a component of a solution divided by the total number of moles of all components:
Example 9.14. The Pressure of a Mixture of Gases
A 10.0-L vessel contains 2.50 × 10−3 mol of H2, 1.00 × 10−3 mol of He, and 3.00 × 10−4 mol of Ne at 35°C.
(a) What are the partial pressures of each of the gases?
(b) What is the total pressure in atmospheres?
Solution
(a) The gases behave independently, so the partial pressure of each gas can be determined from the ideal gas equation, using [latex]P = \frac {nRT}{V}[/latex]:
[latex]P_{Ne} = \frac {(3.00 \times 10^{-4} \: \cancel {mol})(0.080206 \: \cancel {L} \cdot atm/\cancel {mol} \cdot \cancel {K})(308 \: \cancel {K})}{10.0 \: \cancel {L}} = 7.58 \times 10^{-4} \: atm[/latex]
[latex][/latex]
(b) The total pressure is given by the sum of the partial pressures:
Check Your Learning
A 5.73-L flask at 25°C contains 0.0388 mol of N2, 0.147 mol of CO, and 0.0803 mol of H2. What is the total pressure in the flask in atmospheres?
Click here to see the solution!
1.137 atm
Because the identity of the gas does not matter for the total pressure, we can calculate the total pressure if we know the total number of mols of gas in the container:
[latex]n_T = n_{N_2} + n_{CO} + n_{H_2} = 0.0388 \: mol + 0.147 \: mol + 0.0803 \: mol[/latex]
[latex]= 0.2661 \: mol[/latex]
[latex]P_{T} = \frac {(0.2661 \: \cancel {mol})(0.080206 \: \cancel {L} \cdot atm/\cancel {mol} \cdot \cancel {K})((25 + 273) \: \cancel {K})}{5.73 \: \cancel {L}} = 1.137 atm[/latex]
Note that you could have solved for the individual partial pressures and added them like in the example above—but this would have required several additional steps!
Here is another example of this concept, this time dealing with mole fraction calculations.
Example 9.15. The Pressure of a Mixture of Gases
A gas mixture used for anesthesia contains 2.83 mol oxygen, O2, and 8.41 mol nitrous oxide, N2O. The total pressure of the mixture is 192 kPa.
(a) What are the mole fractions of O2 and N2O?
(b) What are the partial pressures of O2 and N2O?
Solution
The mole fraction is given by
and the partial pressure is
For O2,
and
For N2O,
and
Check Your Learning
What is the pressure of a mixture of 0.200 g of H2, 1.00 g of N2, and 0.820 g of Ar in a container with a volume of 2.00 L at 20°C?
1.87 atm
Collection of Gases Over Water
A simple way to collect gases that do not react with water is to capture them in a bottle that has been filled with water and inverted into a dish filled with water. The pressure of the gas inside the bottle can be made equal to the air pressure outside by raising or lowering the bottle. When the water level is the same both inside and outside the bottle (Figure 9.22), the pressure of the gas is equal to the atmospheric pressure, which can be measured with a barometer.
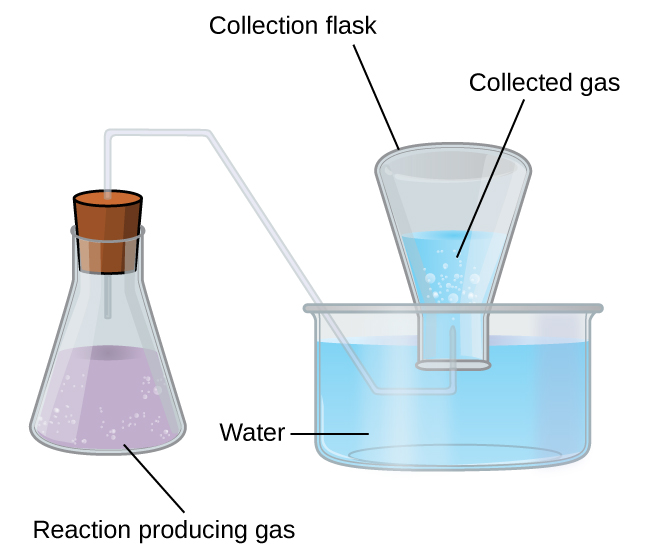
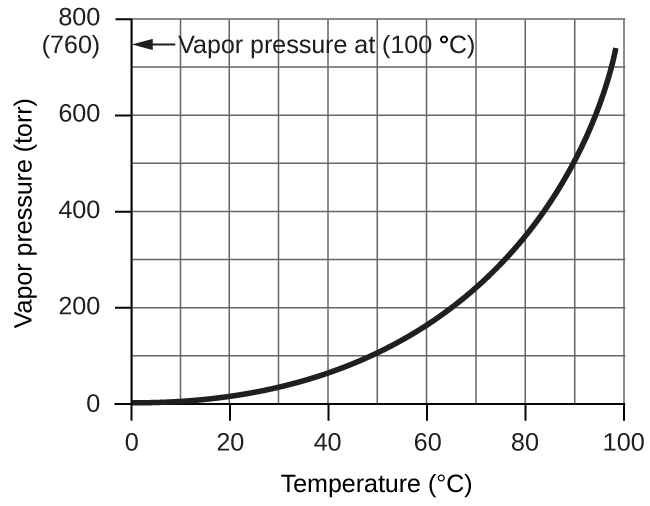
However, there is another factor we must consider when we measure the pressure of the gas by this method. Water evaporates and there is always gaseous water (water vapor) above a sample of liquid water. As a gas is collected over water, it becomes saturated with water vapor and the total pressure of the mixture equals the partial pressure of the gas plus the partial pressure of the water vapor. The pressure of the pure gas is therefore equal to the total pressure minus the pressure of the water vapor—this is referred to as the “dry” gas pressure, that is, the pressure of the gas only, without water vapor. The vapor pressure of water, which is the pressure exerted by water vapor in equilibrium with liquid water in a closed container, depends on the temperature (Figure 9.23); more detailed information on the temperature dependence of water vapor can be found in Table 9.2, and vapor pressure will be discussed in more detail in the next chapter on liquids.
Example 9.16. Pressure of a Gas Collected Over Water
If 0.200 L of argon is collected over water at a temperature of 26°C and a pressure of 750 torr in a system like that shown in Figure 9.21, what is the partial pressure of argon?
Solution
According to Dalton’s law, the total pressure in the bottle (750 torr) is the sum of the partial pressure of argon and the partial pressure of gaseous water:
Rearranging this equation to solve for the pressure of argon gives:
[latex]P_{Ar} = P_T - P_{H_2O}[/latex]
The pressure of water vapor above a sample of liquid water at 26°C is 25.2 torr (Appendix E), so:
Check Your Learning
A sample of oxygen collected over water at a temperature of 29.0°C and a pressure of 764 torr has a volume of 0.560 L. What volume would the dry oxygen from this sample have under the same conditions of temperature and pressure?
Click here for the solution!
0.538 L
The pressure of water vapor above a sample of liquid water at 29.0°C is 30.0 torr (Appendix E), so:
We can now use the partial pressure of O2 and Charles’ law to calculate the volume in the absence of water:
[latex]P_1 V_1 = P_2 V_2[/latex]
[latex]V_2 = \frac{P_1 V_1} {P_2} = \frac{(734 \: torr)(0.560 \: L)}{764 \: torr} = 0.538 \: L[/latex]
Alternatively, you could calculate the mols of O2 using PO2 and the initial volume and pressure, then calculate the new volume using the ideal gas law.
Chemical Stoichiometry and Gases
Chemical stoichiometry describes the quantitative relationships between reactants and products in chemical reactions.
We have previously measured quantities of reactants and products using masses for solids and volumes in conjunction with molarity for solutions; now we can also use gas volumes to indicate quantities. If we know the volume, pressure, and temperature of a gas, we can use the ideal gas equation to calculate how many moles of the gas are present. If we know how many moles of a gas are involved, we can calculate the volume of a gas at any temperature and pressure.
Avogadro’s Law Revisited
Sometimes we can take advantage of a simplifying feature of the stoichiometry of gases that solids and solutions do not exhibit: All gases that show ideal behavior contain the same number of molecules in the same volume (at the same temperature and pressure). Thus, the ratios of volumes of gases involved in a chemical reaction are given by the coefficients in the equation for the reaction, provided that the gas volumes are measured at the same temperature and pressure.
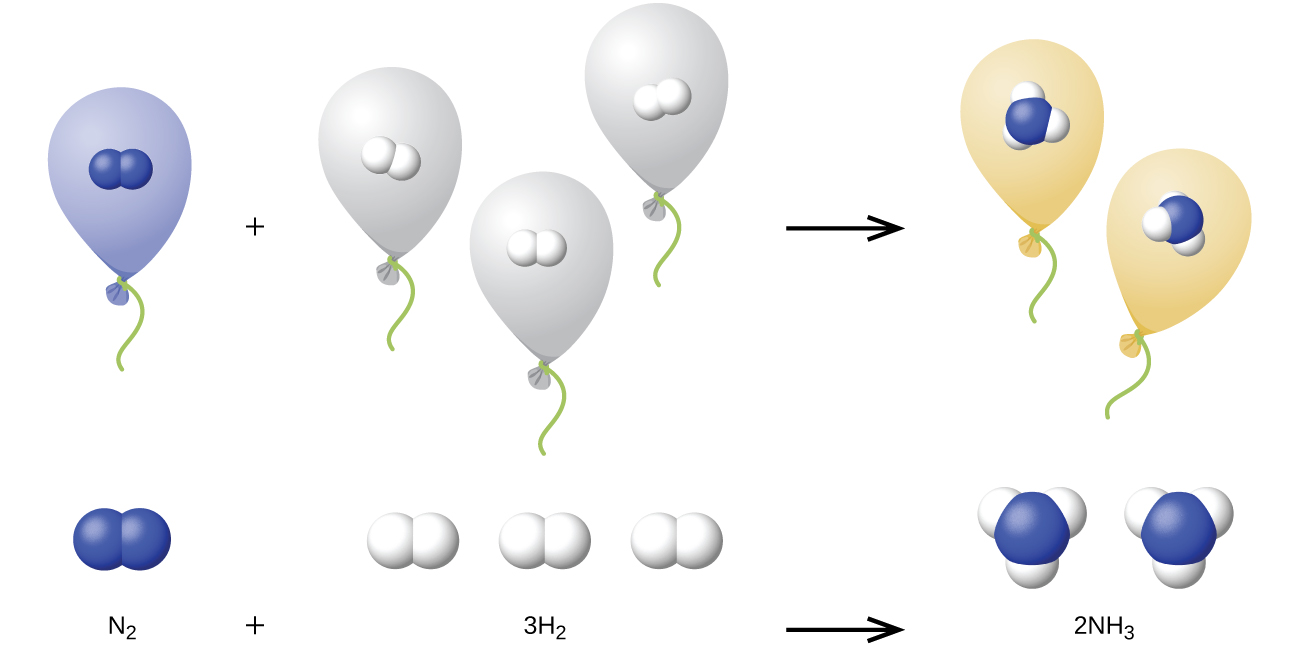
We can extend Avogadro’s law (that the volume of a gas is directly proportional to the number of moles of the gas) to chemical reactions with gases: Gases combine, or react, in definite and simple proportions by volume, provided that all gas volumes are measured at the same temperature and pressure. For example, a given volume of nitrogen gas reacts with three times that volume of hydrogen gas to produce two times that volume of ammonia gas, if pressure and temperature remain constant, since nitrogen and hydrogen gases react to produce ammonia gas according to the following:
The explanation for this is illustrated in Figure 9.24. According to Avogadro’s law, equal volumes of gaseous N2, H2, and NH3, at the same temperature and pressure, contain the same number of molecules. Because one molecule of N2 reacts with three molecules of H2 to produce two molecules of NH3, the volume of H2 required is three times the volume of N2, and the volume of NH3 produced is two times the volume of N2.
Example 9.17. Reaction of Gases
Propane, C3H8(g), is combusted in gas grills to provide the heat for cooking. What volume of O2(g) measured at 25°C and 760 torr is required to react with 2.7 L of propane measured under the same conditions of temperature and pressure? Assume that the propane undergoes complete combustion.
Solution
The ratio of the volumes of C3H8 and O2 will be equal to the ratio of their coefficients in the balanced equation for the reaction:
C3H8(g) + 5 O2(g)→3 CO3(g) + 4 H2O(l)
1 volume + 5 volumes 3 volumes + 4 volumes
From the equation, we see that one volume of C3H8 will react with five volumes of O2:
[latex][/latex]
A volume of 13.5 L of O2 will be required to react with 2.7 L of C3H8.
Check Your Learning
Example 9.18. Volumes of Reacting Gases
Ammonia is an important fertilizer and industrial chemical. Suppose that a volume of 683 billion cubic feet of gaseous ammonia, measured at 25°C and 1 atm, was manufactured. What volume of H2(g), measured under the same conditions, was required to prepare this amount of ammonia by reaction with N2?
Solution
Because equal volumes of H2 and NH3 contain equal numbers of molecules and each three molecules of H2 that react produce two molecules of NH3, the ratio of the volumes of H2 and NH3 will be equal to 3:2. Two volumes of NH3, in this case in units of billion ft3, will be formed from three volumes of H2:
The manufacture of 683 billion ft3 of NH3 required 1,020 billion ft3 of H2. (At 25°C and 1 atm, this is the volume of a cube with an edge length of approximately 1.9 miles.)
Check Your Learning
What volume of O2(g) measured at 25°C and 760 torr is required to react with 17.0 L of ethylene, C2H4(g), measured under the same conditions of temperature and pressure? The products are CO2 and water.
Click here to see the ethylene combustion reaction!
C2H4(g) + 3 O2(g) → 2 CO2(g) + 2 H2O(l)
Click here to see the answer!
[latex]V_{O_2} = 17.0 \: L \times \frac{3 \: L \: O_2}{1 \: L \: ethylene} = 51.0 \: L[/latex]
Example 9.19. Volume of Gaseous Product
What volume of hydrogen at 27°C and 723 torr may be prepared by the reaction of 8.88 g of gallium with an excess of hydrochloric acid?
Solution
Convert the provided mass of the limiting reactant, Ga, to moles of hydrogen produced:
Convert the provided temperature and pressure values to appropriate units (K and atm, respectively), and then use the molar amount of hydrogen gas and the ideal gas equation to calculate the volume of gas:
Check Your Learning
Sulfur dioxide is an intermediate in the preparation of sulfuric acid. What volume of SO2 at 343°C and 1.21 atm is produced by burning l.00 kg of sulfur in excess oxygen?
Click here for the appropriate chemical equation!
S(s) + O2(g) → SO2(g)
Click here for the solution!
Convert the provided mass of the limiting reactant, sulfur (S), to moles of SO2 produced:
Convert the provided temperature to an appropriate unit (K), and then use the molar amount of SO2 gas and the ideal gas equation to calculate the volume of gas:
How Sciences Interconnect
Greenhouse Gases and Climate Change
The thin skin of our atmosphere keeps Earth from being an ice planet and makes it habitable. In fact, this is due to less than 0.5% of the gas molecules present in our atmosphere. Of the energy from the sun that reaches the earth, about 30% is reflected back into space, with the rest absorbed by the atmosphere and the surface of the earth. Some of the energy that the earth absorbs is re-emitted as infrared (IR) radiation, a portion of which passes through the atmosphere back into space. Most if this IR radiation, however, is absorbed by certain atmospheric gases, which in turn re-emit the radiation back towards Earth’s surface (Figure 9.25). This phenomenon, known as the greenhouse effect, maintains global temperatures within the range needed to sustain life on Earth. Without our atmosphere, the earth’s average temperature would be lower by more than 30°C (nearly 60°F). The major greenhouse gases (GHGs) are water vapor, carbon dioxide, methane, nitrous oxide, and ozone.
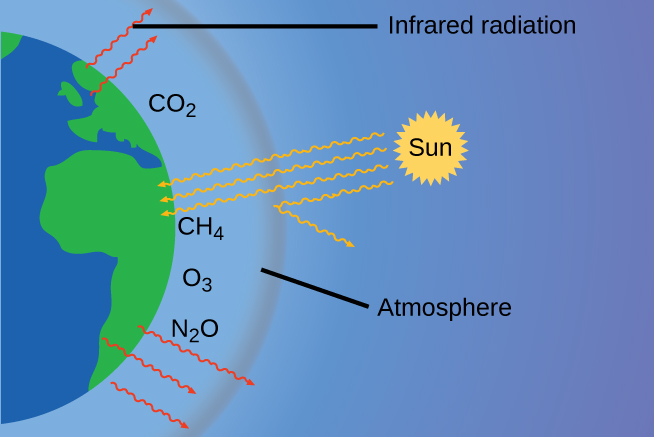
While historical records credit Irish physicist John Tyndall for being the first to show that CO2 and H2O can absorb IR radiation in 1859, this acclaim should go to American amateur scientist Eunice Newton Foote and her work in 1856 (Figure 9.26). Foote submitted her findings to the American Association for the Advancement of Science (AAAS) and Joseph Henry presented her research on her behalf at the meeting. No woman had ever presented before; it is not obvious whether a woman scientist would have been given the opportunity. Her work was written up in Scientific American, the Annual of Scientific Discovery, and a German publication where they mistook her for a man. Foote even speculated about how this warming could affect our atmosphere: “An atmosphere of that gas would give to our earth a much higher temperature; and if there once was, as some suppose, a larger proportion of that gas in the air, an increased temperature must have accompanied it…”[1] It’s unclear if Tyndall was aware of Foote’s accomplishment. Because he had access to the latest scientific equipment of the day, he was able to advance these discoveries much further than Foote had.

Climate scientists call the factors (both natural and anthropogenic) that influence Earth’s energy balance radiative forcings. Greenhouse gases represent the most dominant anthropogenic forcing. In fact, the modern impact of all GHGs on Earth’s increase in temperature is 2.5 times larger than all other forcings combined. This modern increase in GHG emissions started in the mid-1800s and is attributed to human activity such as agriculture, mining, industry, and transportation. Data collected from Antarctic ice cores shows that the concentrations of greenhouse gases, such as carbon dioxide, methane, and nitrous oxide, are significantly higher than at any point in the past 1 million years (Figure 9.27). In recent years, the GHG concentrations are accelerating. For example, CO2 concentration has increased from preindustrial levels of ~280 ppm to more than 420 ppm today.
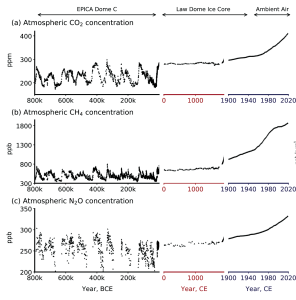
With the increase in GHG concentrations, the Earth’s energy balance has changed, thus altering the Earth’s climate. In fact, Earth’s temperature has risen by an average of 0.06°C (0.11°F) per decade since 1850, or about 1°C (2°F) in total. The 10 warmest years in the historical record have all occurred in the past decade (2014 to 2023) (Figure 9.28). It is important to realize that an average increase in global temperature does not mean that every place is 1°C warmer today than it was in 1850. In fact, many regions have experienced a little warming and others have cooled. Yet there are places, particularly in the higher latitudes, that have experienced greater-than-average warming.
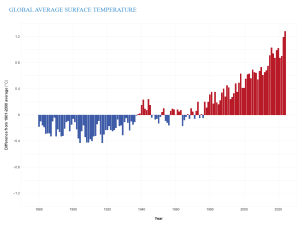
Figure 9.28. Annual surface temperature from 1880 to 2023 compared to the 20th-century average (1901 to 2000). Blue bars indicate cooler-than-average years; red bars show warmer-than-average years. (credit: Global Average Surface Temperature © NOAA Climate.gov is licensed under a CC BY (Attribution) license)
Link to Learning
Click here to see a visualization of Earth’s changing temperature (scroll down to see the video).
Portrait of a Chemist
Katharine Hayhoe
Dr. Katharine Hayhoe is a climate scientist who has authored more than 125 peer-reviewed publications, numerous key national climate reports and hosted PBS Digital Series Global Weirding. She is now the Chief Scientist at The Nature Conservancy and a distinguished professor and endowed chair at Texas Tech University. Dr. Hayhoe’s current research involves looking at future climate scenarios at a local level to see what different choices can be made to protect agriculture, ecosystems, energy, infrastructure, public health, and water resources.
Named one of Time Magazine’s top 100 Most Influential People in 2014, Dr. Hayhoe might be best known for her climate science communication and advocacy for environmental action, including helping us talk to each other about climate change. Using her personal life as an example, she also works to bridge the gap between scientists and Christians.
“As a Christian, I believe we’re called to love others as we’ve been loved by God, and that means caring for those who are suffering—their physical needs and their well-being—which today are being exacerbated by climate impacts. How could I not want to do something about that? That’s why I became a climate scientist.”[2]
Media Attributions
- Eunice Foote & the Oil Barons Cartoon © Chris Slane is licensed under a CC BY-SA (Attribution ShareAlike) license
- Excerpt from a summary of Foote's paper that was reported by David A. Wells in the 1857 volume of his Annual of Scientific Discovery ↵
- Excerpt from Saving Us: A Climate Scientist's Case for Hope and Healing in a Divided World, published by One Signal/Atria Books, a division of Simon & Schuster, Inc. Copyright © 2021 by Katharine Hayhoe. ↵
