4.5 Membrane Potential

All animal cells are surrounded by a plasma membrane composed of a lipid bilayer that regulates the entry and exit of substances from the cell. Due to the action of ion pumps, symporters, antiporters, and channels, the composition of ions inside the cell is different from the composition outside the cell. This difference in ion composition forms the basis of a cell’s membrane potential, or the difference in charge inside versus outside the cell. The membrane potential has two basic functions. First, it allows a cell to function as a battery, providing power in the form of an electrochemical gradient to operate a variety of “molecular devices” embedded in the membrane. Second, in electrically excitable cells such as neurons and muscle cells, it is used for transmitting signals between different parts of a cell. Signals are generated by opening or closing of ion channels at one point in the membrane, producing a local change in the membrane potential that causes electric current to flow rapidly to other points in the membrane.

Membrane Potential

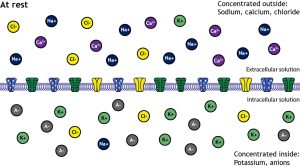
As discussed in Chapter 4.1, the composition of the intracellular fluid (ICF) and the extracellular fluid (ECF) surrounding the cell differs greatly in the concentration of different ions inside and outside the cell. Specifically, the ECF has higher concentrations of sodium (Na⁺), calcium (Ca²⁺), and chloride (Cl^–), while the ICF has higher concentrations of potassium (K⁺) and fixed anions like proteins and nucleic acids (Figure 4.5.1).

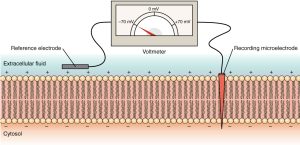
This difference in electrical charge between the interior and the exterior of a biological cell results in the cell’s membrane potential (also transmembrane potential or membrane voltage). A cell’s membrane potential can be directly measured using a voltmeter and two recording electrodes, one placed outside the cell and the other placed inside the cell. Membrane potential can then be determined by comparing the charge inside the cell to the charge outside the cell (Figure 4.5.2).

Voltage is the measure of potential energy generated by separated charges. The difference in charge between the interior and exterior of the cell is so small, membrane potential is typically measured in millivolts (1 volt = 1,000 millivolts). The greater the difference in charge between two points, the higher the voltage. In non-excitable cells, and in excitable cells in their baseline states, the membrane potential is held at a relatively stable value called the resting membrane potential (RMP) or resting potential.

For neurons, typical values of the resting potential range from –70 to –80 millivolts (mV); that is, the interior of a cell has a negative baseline voltage of a bit less than one tenth of a volt. The opening and closing of ion channels can induce a departure from the resting potential. This is called a depolarization if the interior voltage becomes more positive (say from –70 mV to –60 mV) or a hyperpolarization if the interior voltage becomes more negative (say from –70 mV to –80 mV). The changes in membrane potential can be small or larger (graded potentials) depending on how many ion channels are activated and what type they are. The ability of neurons to manipulate membrane potential is discussed in greater detail in Chapter 5.

Equilibrium Potential

Each ion is subject to its electrochemical gradient, which is a combination of the concentration gradient for that ion and the attraction or repulsion that ion has to each side of the membrane. For example, the concentration of Na⁺ outside of cells is roughly 10x higher than the concentration of Na⁺ inside the cell, resulting in a steep concentration gradient that favors the movement of Na⁺ into the cell. In addition, Na⁺ is positively charged while the interior of the cell has a slight negative charge; positive charges are attracted to negative charges, so this additional force will drive Na⁺ into the cell as well. However, if the interior of the cell becomes positively charged, the repulsion of like charges will slow or even halt the flow of Na⁺ into the cell.

The membrane potential of the cell at which there is no net movement for a given ion is called the equilibrium potential for that ion. When the equilibrium potential is reached, the concentration gradient and electrical gradient for that ion are in balance such that the ion is not drawn to one side of the membrane or the other. The equilibrium potential for a given ion can be calculated using the Nernst equation, named after German physicist Walther Nernst, who derived this equation in 1887. The simplified form of the equation is as follows:

E_ion = the equilibrium potential for a given ion, in mV
61 = constant representing the universal gas constant, temperature, and Faraday’s constant
z = the valence (total charge) of the ion
[ion]_out = the concentration of the ion outside the cell
[ion]_in = the concentration of the ion inside the cell

Using Na⁺ as an example, Na⁺ has an extracellular concentration of 145 millimolar (mM), an intracellular concentration of 12 mM, and a valence of +1. With these values, the equilibrium potential for sodium is as follows:

If the membrane is permeable, an ion will move across the cell membrane to bring the membrane potential closer to its equilibrium. This means that if a cell had a resting potential of -70 mV and Na⁺ channels were to open, Na⁺ ions would rush into the cell; the positive charges entering would make the interior of the cell more positive, bringing the membrane potential closer to +66 mV. In order to stop Na⁺ from entering the cell, the membrane potential would have to be +66 mV. If the membrane potential exceeded +66 mV, Na⁺ would exit the cell to reach its equilibrium potential.

Potassium has very different conditions. For a typical cell, the extracellular concentration of K⁺ is 5 mM and the intracellular concentration is 155 mM. With these values, the equilibrium potential for K⁺ is as follows:

This means that if the cell was at rest with a membrane potential of -70 mV and K⁺ were to open, K⁺ would exit the cell; the movement of positive charges out of the cell leaves the cell more negatively charged than it was before, which would drive the membrane potential closer to -90 mV.

Membrane Potential and Ion Flow

While there are many charged substances inside and outside a cell that contribute to the resting membrane potential, two ions in particular play a major role in establishing and maintaining the resting membrane potential: Na⁺ and K⁺. Even a cell at rest will have some Na⁺ moving into the cell, either through random opening of Na⁺ leakage channels or as a consequence of secondary active transport. Many cells also have dedicated leakage channels for K⁺ that allow K⁺ to leak out of the cell as well. In general, the presence of K⁺ leakage channels means that the membrane is typically more permeable to K⁺ than to Na⁺. For this reason, the resting membrane potential is typically close to the equilibrium potential for K⁺.

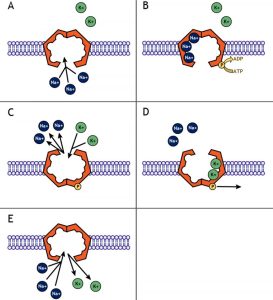
In order to counteract the movement of these cations and maintain a stable resting membrane potential, the sodium-potassium pump functions to maintain the concentration gradients of these ions. The pump moves three Na⁺ ions out of the cell and returns two K⁺ ions into the cell for every ATP consumed (Figure 4.5.3). This pushes more cations out of the cell than are brought in, keeping the interior of the cell more negative relative to the outside environment. Since K⁺ is being returned to the interior of the cell against its gradient, the resting potential is not equal to the equilibrium potential for K⁺ but is slightly more positive at around -70 mV.

Glossary

anion

a negatively charged ion

cation

a positively charged ion

depolarization

a change in membrane potential making the inside of the cell more positive than at rest

electrochemical gradient

the combined effect of an ion’s concentration gradient and the electrical charge gradient across a membrane

equilibrium potential

the membrane voltage at which there is no net movement of a particular ion across the membrane

hyperpolarization

a change in membrane potential that makes the interior of the cell more negative than at rest

leakage channel

an ion channel that is always open, allowing ions to move according to their gradients

membrane potential

the electrical potential difference across the plasma membrane due to ion distribution

Nernst equation

an equation used to calculate the equilibrium potential of an ion based on its concentration gradient and charge

resting membrane potential

the stable membrane voltage of a non-excited cell, typically around –70 mV

voltage

the measure of potential energy caused by separated charges across a membrane

Glossary Flashcards

This work, Human Physiology, is adapted from Anatomy & Physiology by OpenStax, licensed under CC BY, and A and P for STEM Educators by LibreText, licensed under CC BY-SA. This edition, with revised content and artwork, is licensed under CC BY-SA except where otherwise noted.

Images from Anatomy & Physiology by OpenStax are licensed under CC BY except where otherwise noted.

Access the original for free at OpenStax.

Report an Error

Did you find an error, typo, broken link, or other problem in the text? Please follow this link to the error reporting form to submit an error report to the authors.